题目内容
4.计算:(1)($\sqrt{24}$-$\sqrt{\frac{1}{2}}$)-($\sqrt{\frac{1}{8}}$+$\sqrt{6}$);
(2)2$\sqrt{12}$×$\frac{\sqrt{3}}{4}$÷5$\sqrt{2}$;
(3)(2$\sqrt{3}$+6)(2$\sqrt{3}$-$\sqrt{6}$)
(4)(2$\sqrt{48}$-3$\sqrt{27}$)$÷\sqrt{6}$
(5)(2$\sqrt{2}$+3$\sqrt{3}$)2;
(6)($\frac{3}{2}$$\sqrt{1\frac{2}{3}}$-$\sqrt{1\frac{1}{4}}$)2.
分析 (1)先化简,再进一步合并即可;
(2)先化简,再算乘除;
(3)利用二次根式的乘法计算即可;
(4)先化简,合并后再算除法;
(5)(6)利用完全平方公式计算即可.
解答 解:(1)原式=2$\sqrt{6}$-$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{4}$-$\sqrt{6}$
=$\sqrt{6}$-$\frac{3\sqrt{2}}{4}$;
(2)原式=4$\sqrt{3}$×$\frac{\sqrt{3}}{4}$÷5$\sqrt{2}$
=3÷5$\sqrt{2}$
=$\frac{3}{10}$$\sqrt{2}$;
(3)原式=12-6$\sqrt{2}$+12$\sqrt{3}$-6$\sqrt{6}$;
(4)原式=(8$\sqrt{3}$-9$\sqrt{3}$)÷$\sqrt{6}$
=-$\sqrt{3}$÷$\sqrt{6}$
=-$\frac{\sqrt{2}}{2}$;
(5)原式=8+12$\sqrt{6}$+27
=35+12$\sqrt{6}$;
(6)原式=$\frac{9}{4}$×$\frac{5}{3}$-2×$\frac{3}{2}$$\sqrt{1\frac{2}{3}}$×$\sqrt{1\frac{1}{4}}$+$\frac{5}{4}$
=5-$\frac{5}{2}$$\sqrt{3}$.
点评 此题考查二次根式的混合运算,掌握二次根式化简方法和运算方法是解决问题的关键.

练习册系列答案
相关题目
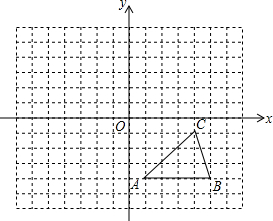 如图,在平面直角坐标系中,△ABC为格点三角形(顶点都是格点)且C(4,-1)
如图,在平面直角坐标系中,△ABC为格点三角形(顶点都是格点)且C(4,-1)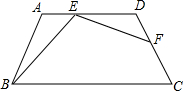 在梯形ABCD中,AD∥BC.AB=DC=AD=6,∠ABC=60°,点E、F分别在AD、DC上(点E与A、D不重合);且∠BEF=120°,设AE=x,DF=y.
在梯形ABCD中,AD∥BC.AB=DC=AD=6,∠ABC=60°,点E、F分别在AD、DC上(点E与A、D不重合);且∠BEF=120°,设AE=x,DF=y.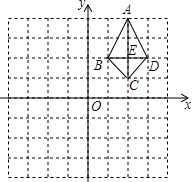 如图,四边形ABCD的对角线AC、BD相交于点E.
如图,四边形ABCD的对角线AC、BD相交于点E.