题目内容
9.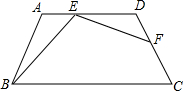 在梯形ABCD中,AD∥BC.AB=DC=AD=6,∠ABC=60°,点E、F分别在AD、DC上(点E与A、D不重合);且∠BEF=120°,设AE=x,DF=y.
在梯形ABCD中,AD∥BC.AB=DC=AD=6,∠ABC=60°,点E、F分别在AD、DC上(点E与A、D不重合);且∠BEF=120°,设AE=x,DF=y.(1)求证:△ABE∽△DEF;
(2)求出 y关于x的函数关系;
(3)当x为何值时,y有最大值,最大值为多少?
分析 (1)由AD∥BC,AB=DC,∠ABC=60°,由等腰梯形的性质可得∠A=∠D,等量代换易得∠A=∠BEF,可得∠DEF=∠ABE,证得结论;
(2)由△ABE∽△DEF,利用相似三角形对应边的比相等,得出y关于x的函数关系;
(3)利用配方法,将(2)中的函数关系式写成顶点式,可求最大值.
解答 (1)证明:∵AD∥BC,AB=DC,∠ABC=60°,
∴∠A=∠D,∠A=120°
∵∠BEF=120°,
∴∠A=∠BEF,
又∵∠AEB+∠BEF+∠DEF=180°,
在△AEB中,∠AEB+∠A+∠ABE=180°,
∴∠DEF=∠ABE,
∴△ABE∽△DEF;
(2)解:∵△ABE∽△DEF,
∴$\frac{AB}{DE}$=$\frac{AE}{DF}$,即$\frac{6}{6-x}$=$\frac{x}{y}$,
解得y=-$\frac{1}{6}$x2+x;
(3)解:∵y=-$\frac{1}{6}$x2+x=y=-$\frac{1}{6}$(x-3)2+$\frac{3}{2}$,且-$\frac{1}{6}$<0,
∴当x=3时,y最大值=$\frac{3}{2}$.
点评 本题考查了等腰梯形的性质与二次函数的综合运用.关键是利用相似三角形的性质得出x、y的关系式.

练习册系列答案
相关题目
19.下列说法中,不正确的是( )
| A. | 三角形的内心是三角形三条内角平分线的交点 | |
| B. | 锐角三角形、直角三角形、钝角三角形的内心都在三角形内部 | |
| C. | 垂直于半径的直线是圆的切线 | |
| D. | 三角形的内心到三角形的三边的距离相等 |
 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,求BE的长.
如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,求BE的长.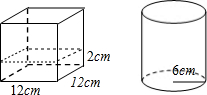 如图所示,一个底面为正方形的容器中盛有高度为2cm的液体,正方形的边长为12cm,把这些液体倒入底面半径为6cm的圆柱形容器中,求液体的高度.(结果保留π)
如图所示,一个底面为正方形的容器中盛有高度为2cm的液体,正方形的边长为12cm,把这些液体倒入底面半径为6cm的圆柱形容器中,求液体的高度.(结果保留π)