题目内容
9.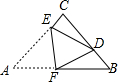 如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为$\frac{1}{3}$.
如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为$\frac{1}{3}$.
分析 由折叠可得△AEF≌△DEF,即可得到∠EDF=∠A;由三角形的内角和定理及平角的知识即可得到∠CDE=∠BFD,最后根据sin∠CDE=$\frac{CE}{ED}$进行计算,即可解决问题.
解答  解:∵在△ABC中,∠ACB=90°,AC=BC=4,
解:∵在△ABC中,∠ACB=90°,AC=BC=4,
∴∠A=∠B,
由折叠的性质得到:△AEF≌△DEF,
∴∠EDF=∠A,
∴∠EDF=∠B,
∴∠CDE+∠BDF+∠EDF=∠BFD+∠BDF+∠B=180°,
∴∠CDE=∠BFD.
又∵AE=DE=3,
∴CE=4-3=1,
∴在直角△ECD中,sin∠CDE=$\frac{CE}{ED}$=$\frac{1}{3}$,
∴sin∠BFD=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 主要考查了翻折变换的性质,解题的关键是灵活运用全等三角形的性质、三角形的内角和定理等知识.折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
10.某公司开发两种新产品,A型产品600件,B型产品400件,分配到甲、乙两地试销,其中甲地销售700件,乙地销售300件,两地销售这两种产品每件的利润(元)如表
设分配到甲地A型产品x件,公司售完这1000件产品的总利润为W(元)
(1)求W关于x的函数关系式,并求出最大利润是多少?
(2)为了加快A型产品的销售,公司决定对A型产品加强广告宣传,由于销售成本增加,A型产品的每件销售利润有所降低,甲地的每件销售利润降低$\frac{x}{100}$元,乙地的每件销售利润降低2元,那么公司售完这1000件产品最小可以获得多少利润?
| A型利润 | B型利润 | |
| 甲地 | 20 | 17 |
| 乙地 | 16 | 15 |
(1)求W关于x的函数关系式,并求出最大利润是多少?
(2)为了加快A型产品的销售,公司决定对A型产品加强广告宣传,由于销售成本增加,A型产品的每件销售利润有所降低,甲地的每件销售利润降低$\frac{x}{100}$元,乙地的每件销售利润降低2元,那么公司售完这1000件产品最小可以获得多少利润?
1.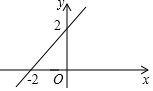 一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是( )
一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是( )
 一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是( )
一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是( )| A. | x>-2 | B. | x>0 | C. | x<-2 | D. | x<0 |
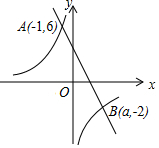 如图,在直角坐标系xoy中,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,6)、B(a,-2)两点.
如图,在直角坐标系xoy中,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,6)、B(a,-2)两点. 如图,已知△ABC 和△FED,B,D,C,E 在一条直线上,∠B=∠E,AB=FE,BD=EC.证明AC∥DF.
如图,已知△ABC 和△FED,B,D,C,E 在一条直线上,∠B=∠E,AB=FE,BD=EC.证明AC∥DF.
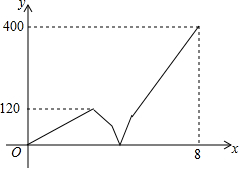 一条笔直的公路上顺次有A、B、C三地,甲车从B地出发往A地匀速行驶,到达A地后停止,在甲车出发的同时,乙车从B地出发往A地匀速行驶,到达A地停留1小时后,调头按原速向C地行驶,若AB两地相距300千米,在两车行驶的过程中,甲、乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则在他们出发后经过4$\frac{3}{8}$小时相遇.
一条笔直的公路上顺次有A、B、C三地,甲车从B地出发往A地匀速行驶,到达A地后停止,在甲车出发的同时,乙车从B地出发往A地匀速行驶,到达A地停留1小时后,调头按原速向C地行驶,若AB两地相距300千米,在两车行驶的过程中,甲、乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则在他们出发后经过4$\frac{3}{8}$小时相遇.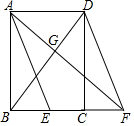 如图,在矩形ABCD中,AD=1,平行四边形AEFD是矩形ABCD的伴随四边形,且E是BC的中点,若AF⊥BD,求AB的值.
如图,在矩形ABCD中,AD=1,平行四边形AEFD是矩形ABCD的伴随四边形,且E是BC的中点,若AF⊥BD,求AB的值.