题目内容
10.某公司开发两种新产品,A型产品600件,B型产品400件,分配到甲、乙两地试销,其中甲地销售700件,乙地销售300件,两地销售这两种产品每件的利润(元)如表| A型利润 | B型利润 | |
| 甲地 | 20 | 17 |
| 乙地 | 16 | 15 |
(1)求W关于x的函数关系式,并求出最大利润是多少?
(2)为了加快A型产品的销售,公司决定对A型产品加强广告宣传,由于销售成本增加,A型产品的每件销售利润有所降低,甲地的每件销售利润降低$\frac{x}{100}$元,乙地的每件销售利润降低2元,那么公司售完这1000件产品最小可以获得多少利润?
分析 (1)根据“总利润=A产品销往甲地的利润+A产品销往乙地的利润+B产品销往甲地的利润+B产品销往乙地的利润”列出函数解析式,由x的范围可得函数的最值;
(2)根据(1)中的相等关系列出函数解析式,由二次函数的性质结合x的范围可得最值.
解答 解:(1)根据题意,得W=20x+16(600-x)+17(700-x)+15(x-300)=2x+17000,
∵$\left\{\begin{array}{l}{x≥0}\\{600-x≥0}\\{700-x≥0}\\{x-300≥0}\end{array}\right.$,
解得:300≤x≤600,
∵W随x的增大而增大,
∴当x=600时,W取得最大值,最大值为18200;
(2)依题意得W=(20-$\frac{x}{100}$)x+14(600-x)+17(700-x)+15(x-300)
=-$\frac{1}{100}$x2+4x+15800
=-$\frac{1}{100}$(x-200)2+16200,
∵当x>200时,W随x的增大而减小,
由于300≤x≤600,
∴当x=600时,W取得最小值,最小值为14600元,
答:公司售完这1000件产品最小可以获得14600元利润.
点评 本题主要考查二次函数的应用,理解题意找到题目蕴含的相等关系,并据此列出函数解析式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.P是抛物线y=x2-4x+5上一点,过点P作PM⊥x轴,PN⊥y轴,垂足分别是M,N,则PM+PN的最小值是( )
| A. | $\frac{5}{4}$ | B. | $\frac{11}{4}$ | C. | 3 | D. | 5 |
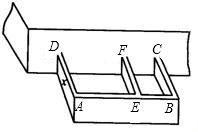 某农户计划利用现有的长为12米的一面墙再修四面墙,建造如图所示的长方体游泳池,培育不同品种的鱼苗,他已备足可以修高为2m,总长24m的墙的材料准备施工,设图中与现有一面墙垂直的三面墙的长度都为m,即AD=BF=BC=xm.(不考虑墙的厚度)
某农户计划利用现有的长为12米的一面墙再修四面墙,建造如图所示的长方体游泳池,培育不同品种的鱼苗,他已备足可以修高为2m,总长24m的墙的材料准备施工,设图中与现有一面墙垂直的三面墙的长度都为m,即AD=BF=BC=xm.(不考虑墙的厚度)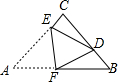 如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为$\frac{1}{3}$.
如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为$\frac{1}{3}$.