题目内容
18.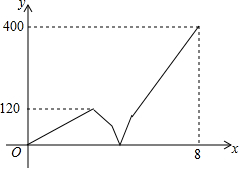 一条笔直的公路上顺次有A、B、C三地,甲车从B地出发往A地匀速行驶,到达A地后停止,在甲车出发的同时,乙车从B地出发往A地匀速行驶,到达A地停留1小时后,调头按原速向C地行驶,若AB两地相距300千米,在两车行驶的过程中,甲、乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则在他们出发后经过4$\frac{3}{8}$小时相遇.
一条笔直的公路上顺次有A、B、C三地,甲车从B地出发往A地匀速行驶,到达A地后停止,在甲车出发的同时,乙车从B地出发往A地匀速行驶,到达A地停留1小时后,调头按原速向C地行驶,若AB两地相距300千米,在两车行驶的过程中,甲、乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则在他们出发后经过4$\frac{3}{8}$小时相遇.
分析 观察函数图象可知A、C两地的间距,由速度=路程÷时间可求出乙车的速度,结合甲、乙两车速度间的关系可求出甲车的速度,再求出乙车从A地返回时,两车的间距,依据相遇时间=4+两车间的间距÷两车速度和,即可求出甲、乙两车相遇的时间.
解答 解:∵最终两车相距400千米,
∴A、C两地相距400千米.
乙车的速度为(300+400)÷(8-1)=100(千米/小时),
乙车从B到达A地的时间为300÷100=3(小时),
甲车的速度为100-120÷3=60(千米/小时),
乙车从A地返回时,两车的间距为300-60×4=60(千米),
两车相遇的时间为4+60÷(100+60)=4$\frac{3}{8}$(小时).
故答案为:4$\frac{3}{8}$.
点评 本题考查了一次函数的应用,观察函数图象结合数量关系,列式计算是解题的关键.

练习册系列答案
相关题目
8.P是抛物线y=x2-4x+5上一点,过点P作PM⊥x轴,PN⊥y轴,垂足分别是M,N,则PM+PN的最小值是( )
| A. | $\frac{5}{4}$ | B. | $\frac{11}{4}$ | C. | 3 | D. | 5 |
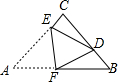 如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为$\frac{1}{3}$.
如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为$\frac{1}{3}$.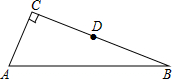 如图,在△ABC中,∠C=90°,AC=5,BC=12,D是BC边的中点.
如图,在△ABC中,∠C=90°,AC=5,BC=12,D是BC边的中点. (1)计算:(a+b)2-b(2a+b)
(1)计算:(a+b)2-b(2a+b) 如图是由5个相同大小的正方体搭成的几何体,则它的俯视图是( )
如图是由5个相同大小的正方体搭成的几何体,则它的俯视图是( )



 如图,每个小方格都是边长为1的小正方形.
如图,每个小方格都是边长为1的小正方形. 如图,在Rt△ABC中,∠A=30°,斜边AC的垂直平分线交AB于D,交AC于E,连接CD,若BD=1,则AD的长是2.
如图,在Rt△ABC中,∠A=30°,斜边AC的垂直平分线交AB于D,交AC于E,连接CD,若BD=1,则AD的长是2.