题目内容
20.某校八年级有316名学生,其中四个班级每班40人,四个班级每班39人,如果对每个班级的每一位学生按1~40或1~39进行编号,在一次问卷调查中,问:(1)在一个40人的班级中任意抽1名学生去答卷,抽到编号个位上数字为“2”“4”和“0”的学生的概率为多少?
(2)在一个39人的班级中任意抽1名学生去答卷,抽列编号个位上数字为“2”“4”和“0”的学生的概率为多少?
(3)在这个年级中任意抽1名学生去答卷,抽到编号个位上数字为“2”“4”和“0”的学生的概率为多少?
分析 (1)根据概率公式确定所有等可能结果数和使该事件发生的结果数,据此可得;
(2)根据概率公式可得答案;
(3)根据概率公式可得答案.
解答 解:(1)在一个40人的班级中任意抽1名学生去答卷,有40种等可能结果,
其中抽到编号个位上数字为“2”“4”和“0”的学生有12种结果,
∴抽到编号个位上数字为“2”“4”和“0”的学生概率为$\frac{12}{40}$=$\frac{3}{10}$;
(2)在一个39人的班级中任意抽1名学生去答卷,有39种等可能结果,
其中抽到编号个位上数字为“2”“4”和“0”的学生有11种结果,
∴抽到编号个位上数字为“2”“4”和“0”的学生概率为$\frac{11}{40}$;
(3)在这个年级中任意抽1名学生去答卷,有316种结果,
其中抽到编号个位上数字为“2”“4”和“0”的学生有12×4+11×4=92种结果,
∴抽到编号个位上数字为“2”“4”和“0”的学生的概率为$\frac{92}{316}$=$\frac{23}{79}$.
点评 本题主要考查概率公式,熟练掌握随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数是解题的关键.

练习册系列答案
相关题目
8.P是抛物线y=x2-4x+5上一点,过点P作PM⊥x轴,PN⊥y轴,垂足分别是M,N,则PM+PN的最小值是( )
| A. | $\frac{5}{4}$ | B. | $\frac{11}{4}$ | C. | 3 | D. | 5 |
12. 如图,直线a∥b,∠1=30°,∠2=40°,且AD=AC,则∠3的度数是( )
如图,直线a∥b,∠1=30°,∠2=40°,且AD=AC,则∠3的度数是( )
 如图,直线a∥b,∠1=30°,∠2=40°,且AD=AC,则∠3的度数是( )
如图,直线a∥b,∠1=30°,∠2=40°,且AD=AC,则∠3的度数是( )| A. | 70° | B. | 40° | C. | 45° | D. | 35° |
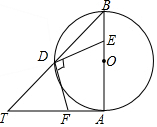 如图,AB是⊙O的直径,AT=AB,∠ABT=45°.
如图,AB是⊙O的直径,AT=AB,∠ABT=45°.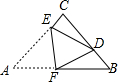 如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为$\frac{1}{3}$.
如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为$\frac{1}{3}$.