题目内容
17.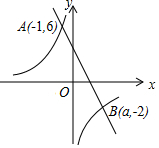 如图,在直角坐标系xoy中,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,6)、B(a,-2)两点.
如图,在直角坐标系xoy中,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,6)、B(a,-2)两点.(1)求一次函数的解析式;
(2)连接OA、OB,求△AOB的面积;
(3)当x满足-1≤x<0时,0<y1≤y2.
分析 (1)利用待定系数法求一次函数的解析式;
(2)利用面积和求△AOB的面积;
(3)观察图形得出.
解答 解:(1)由反比例函数得:-1×6=-2a,
∴a=3,
∴B(3,-2),
把A(-1,6)、B(3,-2)两点的坐标代入y1=k1x+b中得:
$\left\{\begin{array}{l}{-{k}_{1}+b=6}\\{3{k}_{1}+b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=-2}\\{b=4}\end{array}\right.$,
∴一次函数的解析式为:y1=-2x+4;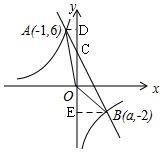
(2)如图,过A作AD⊥y轴于D,过B作BE⊥y轴于E,
y1=-2x+4,
当x=0时,y=4,
∴C(0,4),
∴OC=4,
∴S△AOB=S△AOC+S△BOC=$\frac{1}{2}$OC•AD+$\frac{1}{2}$OC•DE=$\frac{1}{2}$×4×1+$\frac{1}{2}$×4×3=8;
(3)当x满足-1≤x<0时,0<y1≤y2.
故答案为:-1≤x<0.
点评 本题考查了一次函数和反比例函数的交点问题,还考查了利用待定系数法求一次函数和反比例函数的解析式,注意图象与坐标轴围成的图形的面积的求法,利用差或和来求解.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
8.P是抛物线y=x2-4x+5上一点,过点P作PM⊥x轴,PN⊥y轴,垂足分别是M,N,则PM+PN的最小值是( )
| A. | $\frac{5}{4}$ | B. | $\frac{11}{4}$ | C. | 3 | D. | 5 |
12. 如图,直线a∥b,∠1=30°,∠2=40°,且AD=AC,则∠3的度数是( )
如图,直线a∥b,∠1=30°,∠2=40°,且AD=AC,则∠3的度数是( )
 如图,直线a∥b,∠1=30°,∠2=40°,且AD=AC,则∠3的度数是( )
如图,直线a∥b,∠1=30°,∠2=40°,且AD=AC,则∠3的度数是( )| A. | 70° | B. | 40° | C. | 45° | D. | 35° |
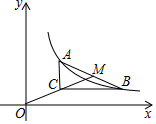 如图,已知点A(2,n),B(6,m)是双曲线y=$\frac{6}{x}$上的两点,分别过点A,B 作x 轴,y 轴的垂线交于点C,OC 的延长线与AB交于点M,则tan∠MCB=$\frac{1}{2}$.
如图,已知点A(2,n),B(6,m)是双曲线y=$\frac{6}{x}$上的两点,分别过点A,B 作x 轴,y 轴的垂线交于点C,OC 的延长线与AB交于点M,则tan∠MCB=$\frac{1}{2}$.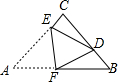 如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为$\frac{1}{3}$.
如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为$\frac{1}{3}$.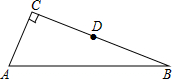 如图,在△ABC中,∠C=90°,AC=5,BC=12,D是BC边的中点.
如图,在△ABC中,∠C=90°,AC=5,BC=12,D是BC边的中点. 如图,每个小方格都是边长为1的小正方形.
如图,每个小方格都是边长为1的小正方形.