题目内容
14．有3张背面完全相同的卡片，正面分别印有如图的几何图形．现将这3张卡片正面朝下摆放并洗匀，从中任意抽取一张记下卡片正面的图形；放回后再次洗匀，从中任意抽取一张，两次抽到的卡片正面的图形都是中心对称图形的概率是$\frac{4}{9}$．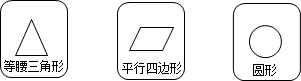
分析 以采用树状图求解．此题为不放回实验，共有9种情况，摸出两张牌面图形都是中心对称图形的纸牌的有4种，所以摸出两张牌面图形都是中心对称图形的纸牌的概率是$\frac{4}{9}$．
解答 解：设A是等腰三角形，B是平行四边形，C是圆，
画树状图得，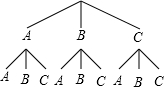
∴一共有9种情况，
∵B与C时中心对称图形，
∴摸出两张牌面图形都是中心对称图形的纸牌有4种；
∴摸出两张牌面图形都是中心对称图形的纸牌的概率是$\frac{4}{9}$，
故答案为：$\frac{4}{9}$．
点评 此题主要考查了树状图法求概率，树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
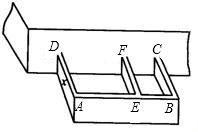某农户计划利用现有的长为12米的一面墙再修四面墙，建造如图所示的长方体游泳池，培育不同品种的鱼苗，他已备足可以修高为2m，总长24m的墙的材料准备施工，设图中与现有一面墙垂直的三面墙的长度都为m，即AD=BF=BC=xm．（不考虑墙的厚度）
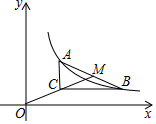如图，已知点A（2，n），B（6，m）是双曲线y=$\frac{6}{x}$上的两点，分别过点A，B 作x 轴，y 轴的垂线交于点C，OC 的延长线与AB交于点M，则tan∠MCB=$\frac{1}{2}$．
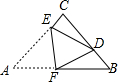如图，在△ABC中，∠ACB=90°，AC=BC=4，将△ABC折叠，使点A落在BC边上的点D处，EF为折痕，若AE=3，则sin∠BFD的值为$\frac{1}{3}$．
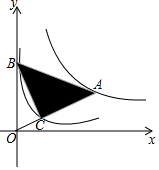如图，点A是反比例函数y=$\frac{k}{x}$（x＞0）的图象上一点，OA与反比例函数y=$\frac{1}{x}$（x＞0）的图象交于点C，点B在y轴的正半轴上，且AB=OA，若△ABC的面积为6，则k的值为9．
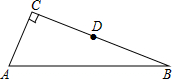如图，在△ABC中，∠C=90°，AC=5，BC=12，D是BC边的中点．
如图是由5个相同大小的正方体搭成的几何体，则它的俯视图是（ ）
