题目内容
17.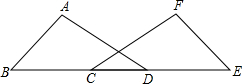 如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠A=∠F.
如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠A=∠F.
分析 先根据SAS判定△ABD≌△FEC,再根据全等三角形的对应角相等,得出∠A=∠F.
解答 证明:∵点B,C,D,E在同一直线上,BC=DE,
∴BC+CD=DE+CD,即:BD=CE,
在△ABD与△FEC中,
∴$\left\{\begin{array}{l}{AB=FE}\\{∠B=∠E}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△FEC(SAS),
∴∠A=∠F.
点评 本题主要考查了全等三角形的判定与性质的综合应用,解题时注意:两边及其夹角对应相等的两个三角形全等.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
5.某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核,三人各项得分如表:
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按50%,30%,20%的比例计入总分.根据规定,请你说明谁将被录用.
| 笔试 | 面试 | 体能 | |
| 甲 | 84 | 78 | 90 |
| 乙 | 85 | 80 | 75 |
| 丙 | 80 | 90 | 73 |
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按50%,30%,20%的比例计入总分.根据规定,请你说明谁将被录用.
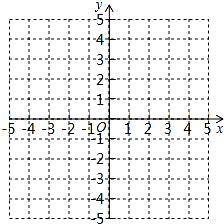 在平面直角坐标系中,A(5,4)、B(4,2)、C(1,0).
在平面直角坐标系中,A(5,4)、B(4,2)、C(1,0).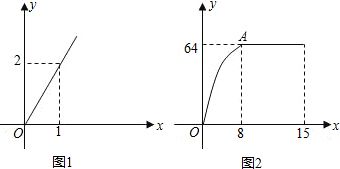
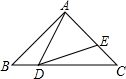 已知:如图,在△ABC中,AB=AC=5cm,BC=6cm,点D在BC边上运动,作∠ADE=∠B,DE交AC于E.
已知:如图,在△ABC中,AB=AC=5cm,BC=6cm,点D在BC边上运动,作∠ADE=∠B,DE交AC于E.