题目内容
9.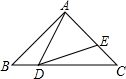 已知:如图,在△ABC中,AB=AC=5cm,BC=6cm,点D在BC边上运动,作∠ADE=∠B,DE交AC于E.
已知:如图,在△ABC中,AB=AC=5cm,BC=6cm,点D在BC边上运动,作∠ADE=∠B,DE交AC于E.(1)求证:△ABD∽△DCE;
(2)当AD=DE时,求BD的长;
(3)当AE=DE时,求BD的长.
分析 (1)欲证明△ABD∽△DCE,只要证明∠BAD=∠CDE,∠B=∠C即可.
(2)当AD=DE时,△ABD≌△DCE,AB=DC=5,由此即可解决问题.
(3)只要证明△CAB∽△CDA,得$\frac{CA}{CD}$=$\frac{CB}{CA}$,求出CD即可解决问题.
解答 (1)证明:∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠BAD+∠B,∠ADC=∠ADE+∠EDC
∵∠ADE=∠B
∴∠BAD=∠EDC,
又∵∠B=∠C
∴△ABD∽△DCE.
(2)解:当AD=DE时,
由(1)知△ABD∽△DCE,
∴△ABD≌△DCE,
∴AB=CD=5,
∴BD=BC-DC=6-5=1.
(3)解:当AE=DE时,可知∠EAD=∠EDA,
∵∠BAD=∠EDC,
∴∠CAB=∠CDA,
又∵∠C=∠C,
∴△CAB∽△CDA,
∴$\frac{CA}{CD}$=$\frac{CB}{CA}$,
∴$\frac{5}{CD}$=$\frac{6}{5}$,
∴CD=$\frac{25}{6}$
∴BD=BC-CD=6-$\frac{25}{6}$=$\frac{11}{6}$.
点评 本题考查相似形综合题、相似三角形的判定和性质,全等三角形得到和性质等知识,解题的关键是正确寻找相似三角形,利用相似三角形的性质解决问题,属于中考常考题型.

练习册系列答案
相关题目
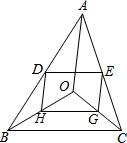 如图,在△ABC中,D、E分别是边AB、AC的中点,O是三角形内部一点,连接OB、OC,G、H分别是OC、OB的中点,试说明四边形DEGH是平行四边形.
如图,在△ABC中,D、E分别是边AB、AC的中点,O是三角形内部一点,连接OB、OC,G、H分别是OC、OB的中点,试说明四边形DEGH是平行四边形.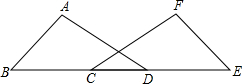 如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠A=∠F.
如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠A=∠F. 如图,?ABCD中,点E、F在直线AC上,BE∥DF.
如图,?ABCD中,点E、F在直线AC上,BE∥DF. 如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,AE=FC.△ABC与△FDE全等吗?说明理由.
如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,AE=FC.△ABC与△FDE全等吗?说明理由.