Question

9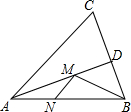．如图，在锐角△ABC中，∠BAC=30°，AB=6，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 在AC上截取AE=AN，先证明△AME≌△AMN（SAS），推出ME=MN．欲求BM+MN最小值，只要求BM+EM的最小值，当B、M、E共线，BE⊥AC时，BM+ME最小．

解答 解：如图，在AC上截取AE=AN，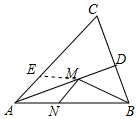
∵∠BAC的平分线交BC于点D，
∴∠EAM=∠NAM，
在△AME与△AMN中，
$\left\{\begin{array}{l}{AE=AN}\\{∠EAM=∠NAM}\\{AM=AM}\end{array}\right.$，
∴△AME≌△AMN（SAS），
∴ME=MN．
∴BM+MN=BM+ME，
欲求BM+MN最小值，只要求BM+EM的最小值，
当B、M、E共线，BE⊥AC时，BM+ME最小，
∵AB=6，∠BAC=30°，
∴BE=$\frac{1}{2}$AB=3，
∴BM+MN的最小值是3．
故选C．

点评 本题考查了轴对称-最短问题、直角三角形30度角性质等知识，解题的关键是能够通过构造全等三角形，把BM+MN进行转化，利用垂线段最短解决问题，属于中考常考题型．