题目内容
19. 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3),△AOB关于y轴对称的图形为△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3),△AOB关于y轴对称的图形为△A1OB1.(1)画出△A1OB1并写出点B1的坐标为(-1,3);
(2)写出△A1OB1的面积为3.5;
(3)点P在x轴上,使△POB是等腰三角形,满足条件的点P共有4个.
分析 (1)确定A、B两点关于y轴对称的对称点位置,再连接即可;
(2)利用矩形面积剪去周围多余三角形的面积即可;
(3)以O为圆心,B1O长为半径画弧可得与x轴有两个交点,B1O的垂直平分线与x轴有一个交点,以B1为圆心,B1O长为半径画弧与x轴有1个交点,这些交点就是P点位置.
解答  解:(1)如图所示:
解:(1)如图所示:
点B1的坐标为(-1,3),
故答案为:(-1,3);
(2)△A1OB1的面积为:3×3-$\frac{1}{2}×$2×3-$\frac{1}{2}$×2×1-$\frac{1}{2}$×1×3=3.5,
故答案为:3.5;
(3)如图所示:满足条件的点P共有4个,
故答案为:4.
点评 此题主要考查了作图--轴对称变换,以及等腰三角形的判定,关键是正确确定组成图形的对称点位置,掌握等腰三角形的判定方法.

练习册系列答案
相关题目
14.已知PA、PB是⊙O的两条切线,切点为A、B,如果OP=4,PA=2$\sqrt{3}$,那么∠OAB等于( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
8.下列说法中,正确的是( )
| A. | 垂线最短 | |
| B. | 两点之间直线最短 | |
| C. | 如果两个角互补,那么这两个角中一个是锐角,一个是钝角 | |
| D. | 同角的补角相等 |
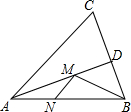 如图,在锐角△ABC中,∠BAC=30°,AB=6,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
如图,在锐角△ABC中,∠BAC=30°,AB=6,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )