题目内容
10.因式分解:ab2-25a=a(b+5)(b-5);计算:4$\sqrt{\frac{1}{2}}$-$\sqrt{8}$=0.分析 原式提取a,再利用平方差公式分解即可;原式化简后,合并即可得到结果.
解答 解:原式=a(b2-25)=a(b+5)(b-5);
原式=4×$\frac{\sqrt{2}}{2}$-2$\sqrt{2}$=2$\sqrt{2}$-2$\sqrt{2}$=0.
故答案为:a(b+5)(b-5);0.
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
1.用“O”摆出如图所示的图案,若按照同样的方式构造图案,则第11个图案需要( )个“O”.


| A. | 100 | B. | 145 | C. | 181 | D. | 221 |
5.已知关于x的不等式组$\left\{\begin{array}{l}{x-a>-1}\\{x-a<2}\end{array}\right.$的解集中任意一个x的值均不在0≤x≤4的范围内,则a的取值范围是( )
| A. | a>5或a<-2 | B. | -2≤a≤5 | C. | -2<a<5 | D. | a≥5或a≤-2 |
19.现要把228吨物资从某地运往甲、乙两地,用大、小两种货车共18辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
(1)求这两种货车各用多少辆?
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的
总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于120吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
| 运往地 车 型 | 甲 地(元/辆) | 乙 地(元/辆) |
| 大货车 | 720 | 800 |
| 小货车 | 500 | 650 |
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的
总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于120吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
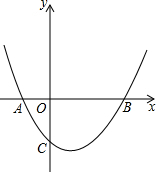 如图,经过点A(-1,0),C(0,-2)的抛物线$y=\frac{1}{2}{x^2}+bx+c$与x轴交于A、B两点,与y轴交于点C
如图,经过点A(-1,0),C(0,-2)的抛物线$y=\frac{1}{2}{x^2}+bx+c$与x轴交于A、B两点,与y轴交于点C
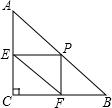 如图,在△ABC中,∠C=90°,AB=10,$\frac{BC}{AC}$=$\frac{3}{4}$,过AB边上一点P作PE⊥AC于点E,PF⊥BC于点F,则EF的最小值是$\frac{24}{5}$.
如图,在△ABC中,∠C=90°,AB=10,$\frac{BC}{AC}$=$\frac{3}{4}$,过AB边上一点P作PE⊥AC于点E,PF⊥BC于点F,则EF的最小值是$\frac{24}{5}$.