题目内容
19.现要把228吨物资从某地运往甲、乙两地,用大、小两种货车共18辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:| 运往地 车 型 | 甲 地(元/辆) | 乙 地(元/辆) |
| 大货车 | 720 | 800 |
| 小货车 | 500 | 650 |
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的
总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于120吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
分析 (1)设大货车用x辆,则小货车用(18-x)辆,根据两种车所在货物是228吨,即可列方程求解;
(2)分别表示出前往甲、乙两地的两种货车的费用的和即可求解;
(3)根据运往甲地的物资不少于120吨,依据运往甲地的物资不少于120吨即可求得a的范围,根据函数的性质求解.
解答 解:(1)设大货车用x辆,则小货车用(18-x)辆,
根据题意得 16x+10(18-x)=228,解得x=8,
∴18-x=18-8=10.
答:大货车用8辆,小货车用10辆;
(2)w=720a+800(8-a)+500(9-a)+650[10-(9-a)]
=70a+11550,
∴w=70a+11550(0≤a≤8且为整数);
(3)由16a+10(9-a)≥120,解得a≥5.
又∵0≤a≤8,
∴5≤a≤8且为整数.
∵w=70a+11550,且70>0,所以w随a的增大而增大,
∴当a=5时,w最小,最小值为w=70×5+11550=11900.
答:使总运费最少的调配方案是:5辆大货车、4辆小货车前往甲地;3辆大货车、6辆小货车前往乙地.最少运费为11900元.
点评 本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.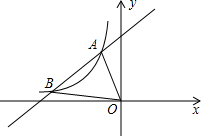 如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx+b交于A(-1,m),B(n,1)两点,则△OAB的面积为( )
如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx+b交于A(-1,m),B(n,1)两点,则△OAB的面积为( )
 如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx+b交于A(-1,m),B(n,1)两点,则△OAB的面积为( )
如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx+b交于A(-1,m),B(n,1)两点,则△OAB的面积为( )| A. | $\frac{11}{2}$ | B. | 4 | C. | $\frac{15}{2}$ | D. | $\frac{13}{2}$ |
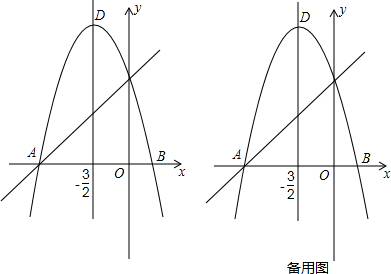
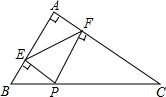 如图,在△ABC中,∠BAC=90°,AB=6,AC=8,点P是BC边上任意一点(B、C除外)PE⊥AB于点E,PF⊥AC于点F,连接EF,则EF的最小值为4.8.
如图,在△ABC中,∠BAC=90°,AB=6,AC=8,点P是BC边上任意一点(B、C除外)PE⊥AB于点E,PF⊥AC于点F,连接EF,则EF的最小值为4.8.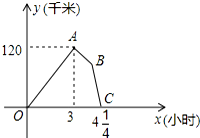 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,则快递车从乙地返回时的速度为90千米/时.
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,则快递车从乙地返回时的速度为90千米/时.