题目内容
5．已知关于x的不等式组$\left\{\begin{array}{l}{x-a＞-1}\\{x-a＜2}\end{array}\right.$的解集中任意一个x的值均不在0≤x≤4的范围内，则a的取值范围是（ ）| A． | a＞5或a＜-2 | B． | -2≤a≤5 | C． | -2＜a＜5 | D． | a≥5或a≤-2 |
分析 根据解不等式组，可得不等式组的解集，根据不等式组的解集是与0≤x≤4的关系，可得答案．
解答 解：解$\left\{\begin{array}{l}{x-a＞-1}\\{x-a＜2}\end{array}\right.$，得
a-1＜x＜a+2，
由不等式组$\left\{\begin{array}{l}{x-a＞-1}\\{x-a＜2}\end{array}\right.$的解集中任意一个x的值均不在0≤x≤4的范围内，得
a+2≤0或a-1≥4，
解得a≥5或a≤-2，
故选：D．
点评 本题考查了不等式的解集，利用解集中任意一个x的值均不在0≤x≤4的范围内得出不等式是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
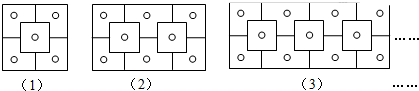
13．用火柴棒按如图的方式搭三角形组成的图形
（1）填写下表：
（2）照这样的规律搭下去，搭20个三角形时要用多少火柴棒？搭n个这样的三角形需要多少火柴棒？
（1）填写下表：
| 三角形个数 | 1 | 2 | 3 | 4 | 5 |
| 火柴棒根数 | 3 | 5 | 7 | 9 | 11 |
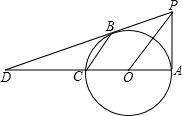以AC=6为直径画一个圆，过点A作AP⊥AC，过点C作CB∥OP，直线PB与直线AC相交于点D．
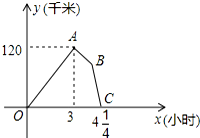某物流公司的快递车和货车同时从甲地出发，以各自的速度匀速向乙地行驶，快递车到达乙地后缷完物品再另装货物共用45分钟，立即按原路以另一速度匀速返回，直至与货车相遇．已知货车的速度为60千米/时，两车之间的距离y（千米）与货车行驶时间x（小时）之间的函数图象如图所示，则快递车从乙地返回时的速度为90千米/时．
如图，直线AB与x轴、y轴分别交于B、A两点，线段OA、OB的长是关于x的一元二次方程x2-14x+48=0的两个根（OA＜OB）