题目内容
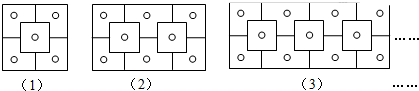
1.用“O”摆出如图所示的图案,若按照同样的方式构造图案,则第11个图案需要( )个“O”.
| A. | 100 | B. | 145 | C. | 181 | D. | 221 |
分析 观察图形可知,从最上一行和最下边一行向中间,“0”的个数是从1开始的连续奇数,然后列出第n个图形中的“0”的个数表达式并根据求和公式计算,再把n=11代入进行计算即可得解.
解答 解:由图可知,第n个图形中“0”的个数为:1+3+5+7+…+(2n-1)+…+7+5+3+1
=2[1+3+5+7+…+(2n-1)]-(2n-1)
=2n2-2n+1,
当n=11时,2n2-2n+1=2×112-2×11+1
=242-22+1
=221.
故选:D.
点评 本题考查图形的变化规律,观察图形得到各行的“0”的个数成连续奇数排列是解题的关键.

练习册系列答案
 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
16.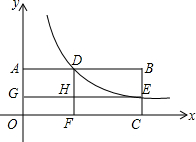 如图,矩形OABC的顶点A在y轴上,C在x轴上,双曲线y=$\frac{k}{x}$与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是1和2,则k的值为( )
如图,矩形OABC的顶点A在y轴上,C在x轴上,双曲线y=$\frac{k}{x}$与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是1和2,则k的值为( )
 如图,矩形OABC的顶点A在y轴上,C在x轴上,双曲线y=$\frac{k}{x}$与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是1和2,则k的值为( )
如图,矩形OABC的顶点A在y轴上,C在x轴上,双曲线y=$\frac{k}{x}$与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是1和2,则k的值为( )| A. | $\frac{12}{5}$ | B. | $\sqrt{2}$+1 | C. | $\frac{5}{2}$ | D. | 2$\sqrt{2}$ |
13.用火柴棒按如图的方式搭三角形组成的图形

(1)填写下表:
(2)照这样的规律搭下去,搭20个三角形时要用多少火柴棒?搭n个这样的三角形需要多少火柴棒?

(1)填写下表:
| 三角形个数 | 1 | 2 | 3 | 4 | 5 |
| 火柴棒根数 | 3 | 5 | 7 | 9 | 11 |
11.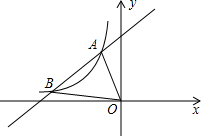 如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx+b交于A(-1,m),B(n,1)两点,则△OAB的面积为( )
如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx+b交于A(-1,m),B(n,1)两点,则△OAB的面积为( )
 如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx+b交于A(-1,m),B(n,1)两点,则△OAB的面积为( )
如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx+b交于A(-1,m),B(n,1)两点,则△OAB的面积为( )| A. | $\frac{11}{2}$ | B. | 4 | C. | $\frac{15}{2}$ | D. | $\frac{13}{2}$ |
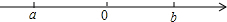 实数a,b在轴上的位置如图所示,化简:$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$.
实数a,b在轴上的位置如图所示,化简:$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$.