题目内容
18.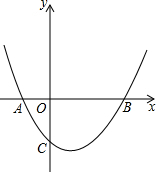 如图,经过点A(-1,0),C(0,-2)的抛物线$y=\frac{1}{2}{x^2}+bx+c$与x轴交于A、B两点,与y轴交于点C
如图,经过点A(-1,0),C(0,-2)的抛物线$y=\frac{1}{2}{x^2}+bx+c$与x轴交于A、B两点,与y轴交于点C(1)求此抛物线的函数解析式和顶点D的坐标;
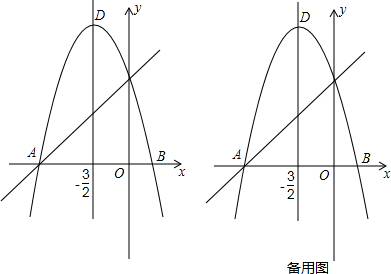
(2)将(1)中求得的抛物线向左平移1个单位长度,再向上平移m(m>0)个单位长度得到新抛物线y1,若新抛物线y1的顶点P在△ABC内,求m的取值范围;
(3)在(1)的结论下,在x轴下方的抛物线上是否存在点P,使得∠APB为锐角?若存在,求出点P的横坐标的取值范围;若不存在,请说明理由.
分析 (1)直接把点A(-1,0),C(0,-2)代入抛物线$y=\frac{1}{2}{x^2}+bx+c$求出b,c的值即可得出其解析式,再求出顶点D的坐标即可;
(2)根据图形平移的性质用m表示出抛物线y1的解析式,根据锐角三角函数的定义得出当x=$\frac{1}{2}$时EF的长即可得出m的取值范围内;
(3)先根据勾股定理判断出△ABC的形状,再根据抛物线的对称性得出∠APB=90°时另一点的坐标,进而可得出结论.
解答 解:(1)∵点A(-1,0),C(0,-2)在抛物线$y=\frac{1}{2}{x^2}+bx+c$上,
∴$\left\{\begin{array}{l}\frac{1}{2}-b+c=0\\ b=-2\end{array}\right.$,解得$\left\{\begin{array}{l}b=-\frac{3}{2}\\ c=-2\end{array}\right.$,
∴抛物线的解析式为y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2,
∴D($\frac{3}{2}$,-$\frac{25}{8}$);
(2)∵由(1)知,抛物线的解析式为y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2,即y=$\frac{1}{2}$(x-$\frac{3}{2}$)2-$\frac{25}{8}$,
∴新抛物线y1的解析式为y=$\frac{1}{2}$(x-$\frac{1}{2}$)2-$\frac{25}{8}$+m,
∴其顶点坐标为($\frac{1}{2}$,m-$\frac{25}{8}$),
∴设抛物线y1的对称轴为直线l,即x=$\frac{1}{2}$.
∵顶点P在△ABC内,B(4,0),
∴新抛物线的顶点在线段EF上,
∵B(4,0),C(0,-2)
∴BE=4-$\frac{1}{2}$=$\frac{7}{2}$,OC=2,
∴$\frac{EF}{BE}$=$\frac{OC}{OB}$,即$\frac{EF}{\frac{7}{2}}$=$\frac{2}{4}$,解得EF=$\frac{7}{4}$,
∵D($\frac{3}{2}$,-$\frac{25}{8}$),$\frac{25}{8}$-$\frac{7}{4}$=$\frac{11}{8}$,
∴$\frac{11}{8}$<m<$\frac{25}{8}$;
(3)∵AC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,BC=$\sqrt{{4}^{2}+{2}^{2}}$=$\sqrt{20}$,AB=4+1=5,
∴△ACB是直角三角形,即∠ACB=90°.
过点C作CG∥x轴,
∵C(0,-2),
∴G(3,-2),
∴当点P与点C或点G重合时∠APB=90°,
∴当点P在点C与点G之间的抛物线上时,∠APB是锐角,
∴点P的横坐标的取值范围为:0<x<3.
点评 本题考查的是二次函数综合题,涉及到二次函数图象上点的坐标特点、锐角三角函数的定义、勾股定理的逆定理等知识,难度较大.


(1)填写下表:
| 三角形个数 | 1 | 2 | 3 | 4 | 5 |
| 火柴棒根数 | 3 | 5 | 7 | 9 | 11 |
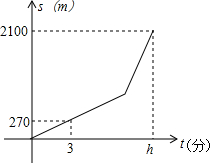 小明从家到学校,开始步行,后来跑步,小明离家的路程S(m)与所用时间t(分)之间的关系如图所示.
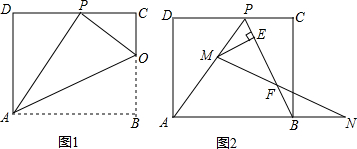
小明从家到学校,开始步行,后来跑步,小明离家的路程S(m)与所用时间t(分)之间的关系如图所示.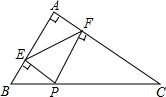 如图,在△ABC中,∠BAC=90°,AB=6,AC=8,点P是BC边上任意一点(B、C除外)PE⊥AB于点E,PF⊥AC于点F,连接EF,则EF的最小值为4.8.
如图,在△ABC中,∠BAC=90°,AB=6,AC=8,点P是BC边上任意一点(B、C除外)PE⊥AB于点E,PF⊥AC于点F,连接EF,则EF的最小值为4.8.