题目内容
11.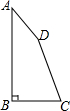 如图,四边形ABCD中,AB⊥BC,∠A+∠B=160°,∠D=4∠C,求四边形ABCD各内角的度数.
如图,四边形ABCD中,AB⊥BC,∠A+∠B=160°,∠D=4∠C,求四边形ABCD各内角的度数.
分析 根据垂直定义可得∠B=90°,根据∠A和∠B的关系可得∠A的度数,再根据四边形内角和定理可得∠C+∠D=200°,再结合∠D=4∠C可得答案.
解答 解:∵AB⊥BC,
∴∠B=90°,
∵∠A+∠B=160°,
∴∠A=70°,
∵∠A+∠B+∠C+∠D=360°,
∴∠C+∠D=200°,
∵∠D=4∠C,
∴∠C=40°,
∴∠D=160°.
点评 此题主要考查了多边形内角,关键是掌握四边形内角和为360°.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
20.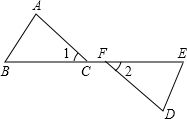 如图,点B,C,F,E在同一直线上,∠1=∠2,BC=FE,要使△ABC≌△DEF,还需添加一个条件,这个条件可以是( )
如图,点B,C,F,E在同一直线上,∠1=∠2,BC=FE,要使△ABC≌△DEF,还需添加一个条件,这个条件可以是( )
 如图,点B,C,F,E在同一直线上,∠1=∠2,BC=FE,要使△ABC≌△DEF,还需添加一个条件,这个条件可以是( )
如图,点B,C,F,E在同一直线上,∠1=∠2,BC=FE,要使△ABC≌△DEF,还需添加一个条件,这个条件可以是( )| A. | AB=DE | B. | ∠B=∠F | C. | BF=CE | D. | ∠A=∠D |
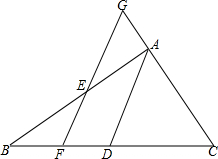 如图,在△ABC中,D是BC的中点,E是线段上的一个动点,(与A、B不重合)过E作AD的平行线,分别与CA的延长线交于G,和BC边交于点F
如图,在△ABC中,D是BC的中点,E是线段上的一个动点,(与A、B不重合)过E作AD的平行线,分别与CA的延长线交于G,和BC边交于点F
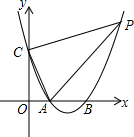 如图,抛物线y=x2-4x+3与x轴交于A,B两点,与y轴交于点C,点P在第一象限的抛物线上,且在对称轴右边,S△PAC=10,求点P的坐标.
如图,抛物线y=x2-4x+3与x轴交于A,B两点,与y轴交于点C,点P在第一象限的抛物线上,且在对称轴右边,S△PAC=10,求点P的坐标. 如图,为了测量校园水平地面上一棵树的高度,数学兴趣小组做了如下的探索:把一面很小的镜子水平放置在离树底(B)7.8米的点E处,然后观察者沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,则树(AB)的高度约为( )米.
如图,为了测量校园水平地面上一棵树的高度,数学兴趣小组做了如下的探索:把一面很小的镜子水平放置在离树底(B)7.8米的点E处,然后观察者沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,则树(AB)的高度约为( )米.