题目内容
17.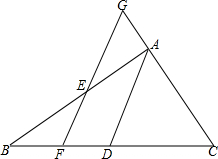 如图,在△ABC中,D是BC的中点,E是线段上的一个动点,(与A、B不重合)过E作AD的平行线,分别与CA的延长线交于G,和BC边交于点F
如图,在△ABC中,D是BC的中点,E是线段上的一个动点,(与A、B不重合)过E作AD的平行线,分别与CA的延长线交于G,和BC边交于点F(1)如果点E是AB的中点,求证:GF+EF=2AD;
(2)如果E不是AB的中点,上述结论还成立吗?说明理由.
分析 (1)由D是BC的中点,得到BD=CD=$\frac{1}{2}$BC,根据三角形的中位线的性质得到BF=DF=$\frac{1}{2}$BD,EF=$\frac{1}{2}$AD,求得$\frac{CD}{CF}$=$\frac{2}{3}$,根据平行线分线段成比例定理得到$\frac{AD}{GF}=\frac{CD}{CF}$=$\frac{2}{3}$,求出GF=$\frac{3}{2}$AD,即可得到结论;
(2)成立,设$\frac{BE}{AB}$=$\frac{1}{n}$,由D是BC的中点,得到BD=CD=$\frac{1}{2}$BC,根据平行线分线段成比例得到$\frac{BF}{BD}$=$\frac{BE}{AB}$=$\frac{EF}{AD}$=$\frac{1}{n}$,求得BF=$\frac{1}{n}$BD,EF=$\frac{1}{n}$AD,证得DF=BD-BF=(1-$\frac{1}{n}$)BD=(1-$\frac{1}{n}$)CD,推出CF=CD+DF=(2-$\frac{1}{n}$)CD,于是得到$\frac{CD}{CF}$=$\frac{1}{2-\frac{1}{n}}$,由平行线分线段成比例得到$\frac{AD}{GF}=\frac{CD}{CF}$=$\frac{1}{2-\frac{1}{n}}$,求得GF=(2-$\frac{1}{n}$)AD,于是得到结论.
解答 解:(1)∵D是BC的中点,
∴BD=CD=$\frac{1}{2}$BC,
∵E是AB的中点,EF∥AD,
∴BF=DF=$\frac{1}{2}$BD,EF=$\frac{1}{2}$AD,
∴BF=DF=$\frac{1}{4}$BC,
∴$\frac{CD}{CF}$=$\frac{2}{3}$,
∵AD∥GF,
∴$\frac{AD}{GF}=\frac{CD}{CF}$=$\frac{2}{3}$,
∴GF=$\frac{3}{2}$AD,
∴GF+EF=$\frac{3}{2}$AD+$\frac{1}{2}$AD=2AD;
(2)成立,
设$\frac{BE}{AB}$=$\frac{1}{n}$,
∵D是BC的中点,
∴BD=CD=$\frac{1}{2}$BC,
∵EF∥AD,
∴$\frac{BF}{BD}$=$\frac{BE}{AB}$=$\frac{EF}{AD}$=$\frac{1}{n}$,
∴BF=$\frac{1}{n}$BD,EF=$\frac{1}{n}$AD,
∴DF=BD-BF=(1-$\frac{1}{n}$)BD=(1-$\frac{1}{n}$)CD,
∴CF=CD+DF=(2-$\frac{1}{n}$)CD,
∴$\frac{CD}{CF}$=$\frac{1}{2-\frac{1}{n}}$,
∵AD∥GF,
∴$\frac{AD}{GF}=\frac{CD}{CF}$=$\frac{1}{2-\frac{1}{n}}$,
∴GF=(2-$\frac{1}{n}$)AD,
∴GF+EF=$\frac{1}{n}$AD+(2-$\frac{1}{n}$)AD=2AD.
点评 本题考查了平行线分线段成比例,三角形的中位线的性质,熟练掌握平行线分线段成比例定理是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{4}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{3\sqrt{13}}{13}$ | D. | $\frac{2\sqrt{13}}{13}$ |
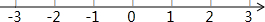 请在数轴上用尺规作出$\sqrt{5}$的对应的点.
请在数轴上用尺规作出$\sqrt{5}$的对应的点.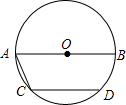 如图,AB是⊙O直径,CD是弦,AB∥CD,且AB=30cm,CD=24cm,求弦AC的长.
如图,AB是⊙O直径,CD是弦,AB∥CD,且AB=30cm,CD=24cm,求弦AC的长.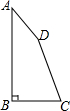 如图,四边形ABCD中,AB⊥BC,∠A+∠B=160°,∠D=4∠C,求四边形ABCD各内角的度数.
如图,四边形ABCD中,AB⊥BC,∠A+∠B=160°,∠D=4∠C,求四边形ABCD各内角的度数.