题目内容
6.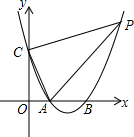 如图,抛物线y=x2-4x+3与x轴交于A,B两点,与y轴交于点C,点P在第一象限的抛物线上,且在对称轴右边,S△PAC=10,求点P的坐标.
如图,抛物线y=x2-4x+3与x轴交于A,B两点,与y轴交于点C,点P在第一象限的抛物线上,且在对称轴右边,S△PAC=10,求点P的坐标.
分析 如图,过点P作PE⊥x轴于点E.将△PAC的面积转化为S△PAC=S梯形OCPE-S△OAC-S△PAE.
解答 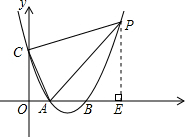 解:∵二次函数的解析式为y=x2-4x+3=(x-3)(x-1),且该函数图象与x轴交于A、B两点,A在B点的左边,与y轴交于C点,
解:∵二次函数的解析式为y=x2-4x+3=(x-3)(x-1),且该函数图象与x轴交于A、B两点,A在B点的左边,与y轴交于C点,
∴A(1,0),B(3,0).
当x=0时,y=3,即C(0,3).
∴OC=3,OA=1,OB=3,AB=2.
如图过点P作PE⊥x轴于点E.设P点的坐标(x,x2-4x+3)(x>0).
则S△PAC=S梯形OCPE-S△OAC-S△PAE=$\frac{1}{2}$(x2-4x+3+3)x-$\frac{1}{2}$×1×3-$\frac{1}{2}$×(x-1)(x2-4x+3)=10.
即x2-x-20=0,
解得x=-4(舍去),或x=5.
当x=5时,y=8.
∴P点坐标是(5,8).
答:P点坐标是(5,8).
点评 本题考查了抛物线与x轴的交点,二次函数的性质.解答该题时,注意转化思想的应用.

练习册系列答案
相关题目
12.点A(-1,-2),点B(3,4),则线段AB与x轴正半轴夹角的正弦值为( )
| A. | $\frac{4}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{3\sqrt{13}}{13}$ | D. | $\frac{2\sqrt{13}}{13}$ |
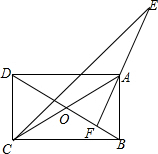 如图,已知矩形ABCD中,AC,BD交于点O,AF⊥BD垂足为F,∠BCD的平分线交FA的延长线于点E,求证:AC=AE.
如图,已知矩形ABCD中,AC,BD交于点O,AF⊥BD垂足为F,∠BCD的平分线交FA的延长线于点E,求证:AC=AE. 如图,四边形ABCD中,AB⊥BC,∠A+∠B=160°,∠D=4∠C,求四边形ABCD各内角的度数.
如图,四边形ABCD中,AB⊥BC,∠A+∠B=160°,∠D=4∠C,求四边形ABCD各内角的度数. 如图,∠AOB=30°,OC平分∠AOB,过点C作CD⊥OA于点D,过点C作CE∥OA交OB于点E.若CE=20cm,求CD的长.
如图,∠AOB=30°,OC平分∠AOB,过点C作CD⊥OA于点D,过点C作CE∥OA交OB于点E.若CE=20cm,求CD的长.