题目内容
1. 如图,为了测量校园水平地面上一棵树的高度,数学兴趣小组做了如下的探索:把一面很小的镜子水平放置在离树底(B)7.8米的点E处,然后观察者沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,则树(AB)的高度约为( )米.
如图,为了测量校园水平地面上一棵树的高度,数学兴趣小组做了如下的探索:把一面很小的镜子水平放置在离树底(B)7.8米的点E处,然后观察者沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,则树(AB)的高度约为( )米.| A. | 15.6 | B. | 6.4 | C. | 3.4 | D. | 3.9 |
分析 利用入射角和反射角相等和余角的等角相等可得到∠AEB=∠CED,则可判断Rt△ABE∽Rt△CDE,然后利用相似比可计算出AB.
解答 解:∵∠AEB=∠CED,
∴Rt△ABE∽Rt△CDE,
∴$\frac{AB}{CD}$=$\frac{BE}{DE}$,即$\frac{AB}{1.6}$=$\frac{7.8}{3.2}$,
∴AB=3.9(m).
故选D.
点评 本题考查了相似三角形的应用:利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9. 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为15cm,则△PAB的周长为( )
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为15cm,则△PAB的周长为( )
 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为15cm,则△PAB的周长为( )
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为15cm,则△PAB的周长为( )| A. | 5cm | B. | 10cm | C. | 20cm | D. | 15cm |
13. 如图,该图案对称轴的条数是( )
如图,该图案对称轴的条数是( )
 如图,该图案对称轴的条数是( )
如图,该图案对称轴的条数是( )| A. | 4条 | B. | 3条 | C. | 2条 | D. | 1条 |
11.下列四个命题中,正确的是( )
| A. | 相似三角形面积的比等于相似比 | |
| B. | 相似三角形对应高的比等于相似比的平方 | |
| C. | 相似三角形对应角平分线的比等于相似比 | |
| D. | 相似三角形中线的比等于相似比 |
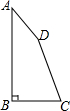 如图,四边形ABCD中,AB⊥BC,∠A+∠B=160°,∠D=4∠C,求四边形ABCD各内角的度数.
如图,四边形ABCD中,AB⊥BC,∠A+∠B=160°,∠D=4∠C,求四边形ABCD各内角的度数.
 如图,∠AOB=30°,OC平分∠AOB,过点C作CD⊥OA于点D,过点C作CE∥OA交OB于点E.若CE=20cm,求CD的长.
如图,∠AOB=30°,OC平分∠AOB,过点C作CD⊥OA于点D,过点C作CE∥OA交OB于点E.若CE=20cm,求CD的长. 如图,在△ABC中,AB=AC,∠C=2∠A,BD平分∠ABC.请找出图中其他的等腰三角形,并选择其中的一个说明理由.
如图,在△ABC中,AB=AC,∠C=2∠A,BD平分∠ABC.请找出图中其他的等腰三角形,并选择其中的一个说明理由.