题目内容
2．对于形如x2+2ax+a2这样的二次三项式，可以用公式法将它分解成（x+α）2的形式．但对于二次三项式x2+2ax-8a2，就不能直接运用公式了．此时，我们可以在二次三项式x2+2ax-8a2中先加上一项a2，使它与x2+2ax的和成为一个完全平方式，再减去a2，整个式子的值不变，于是有：x2+2ax-8a2=（x2+2ax+a2）-a2-8a2=（x+a）2-（3a）2=（x+4a）（x-2a）．像这样，先添一适当项，使式中出现完全平方式，再减去这个项，使整个式子的值不变的方法称为“配方法”．利用以上“配方法”解决：（1）分解因式：a2-6a-16；
（2）当a为何值时，二次三项式a2+4a+5有最小值？
分析 （1）原式利用“配方法”分解即可；
（2）原式利用“配方法”变形后，求出最小值即可．
解答 解：（1）原式=a2-6a+9-25=（a-3）2-25=（a+2）（a-8）；
（2）原式=a2+4a+4+1=（a+2）2+1≥1，
当a+2=0，即a=-2时，原式有最小值．
点评 此题考查了配方法的应用，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
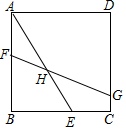如图，在正方形ABCD中，AB=3，E为BC上一点，连接AE，H为AE的中点，过点H作直线FG交AB于F，交CD于G，若∠AHF=30°，AE=FG，则CG的长度为2-$\sqrt{3}$．
11．
如图，在矩形ABCD内部画△ADP，使PA=PD，若∠APD=30°，点P在∠ABC的平分线上，则$\frac{AB}{BC}$的值是（ ）
如图，在矩形ABCD内部画△ADP，使PA=PD，若∠APD=30°，点P在∠ABC的平分线上，则$\frac{AB}{BC}$的值是（ ）| A． | $\frac{3+\sqrt{3}}{2}$ | B． | $\frac{2\sqrt{3}+3\sqrt{2}}{3}$ | C． | $\frac{3\sqrt{3}}{2}$ | D． | $\frac{5\sqrt{2}}{3}$ |