题目内容
15.已知关于x的方程x2-2(m-1)x-m(m+2)=0.(1)求证:方程有两个不相等的实数根;
(2)若x=-2是此方程的一个实数根,求m的值.
分析 (1)根据根的判别式求出△的值,再进行判断即可;
(2)先把x=-2代入方程,然后解关于m的一元二次方程,即可求出m的值.
解答 (1)证明:∵关于x的一元二次方程x2-2(m-1)x-m(m+2)=0.
∴△=4×(m-1)2+4m(m+2)=8m2+4>0,
∴方程总有两个不相等的实数根;
(2)解:∵x=-2是此方程的一个根,
∴把x=-2代入方程中得到4-2(m-1)×(-2)-m(m+2)=0,
∴4+4(m-1)-m(m+2)=0,
∴m2-2m=0,
∴m1=0,m2=2.
点评 此题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
 小明和小亮进行百米赛跑,小明比小亮跑得快.如果两人同时起跑,小明肯定赢.现在小明让小亮先跑若干米.途中l1,l2分别表示两人所跑路程与时间的关系.根据图象回答:
小明和小亮进行百米赛跑,小明比小亮跑得快.如果两人同时起跑,小明肯定赢.现在小明让小亮先跑若干米.途中l1,l2分别表示两人所跑路程与时间的关系.根据图象回答: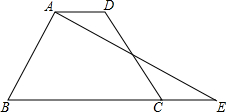 如图,在四边形ABCD中,点F是边CD上一点,连结AF,并延长AF交BC的延长线于点E,使得△ADF与△FCE全等.
如图,在四边形ABCD中,点F是边CD上一点,连结AF,并延长AF交BC的延长线于点E,使得△ADF与△FCE全等.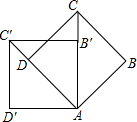 如图,正方形ABCD旋转后得到正方形AB′C′D′,①旋转角是45度;②若AB=1,则C′D=$\sqrt{2}$-1.
如图,正方形ABCD旋转后得到正方形AB′C′D′,①旋转角是45度;②若AB=1,则C′D=$\sqrt{2}$-1.