题目内容
20.把抛物线y=ax2+bx+c向左平移3个单位,向下平移2个单位后,所得抛物线为y=ax2,图象经过点(-1,-$\frac{1}{2}$),求原解析式.分析 把点(-1,-$\frac{1}{2}$)代入抛物线y=ax2求得该抛物线的解析式,易得其顶点坐标,根据平移的规律求得原抛物线的顶点坐标,根据顶点坐标可以写出原抛物线的解析式.
解答 解:把点(-1,-$\frac{1}{2}$)代入y=ax2,得-$\frac{1}{2}$=a.
则平移后的抛物线解析式为y=-$\frac{1}{2}$x2,则其顶点坐标为(0,0).
∵抛物线y=ax2是由抛物线y=ax2+bx+c向左平移3个单位,向下平移2个单位后得到的,
∴抛物线y=ax2+bx+c的顶点坐标是(3,2),
则原抛物线的解析式为:y=-$\frac{1}{2}$(x-3)2+2=-$\frac{1}{2}$x2+3x-$\frac{5}{2}$.
点评 本题考查了二次函数图象与几何变换,平移规律“左加右减,上加下减”求出原抛物线的顶点坐标是解题的关键,利用点的变化确定抛物线的变化更简便.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.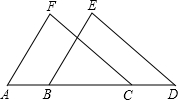 如图所示,△ACF与△BDE全等,点A,B,C,D在同一条直线上,且点F和点E是对应点,点A和点B是对应点,下列结论中,错误的是( )
如图所示,△ACF与△BDE全等,点A,B,C,D在同一条直线上,且点F和点E是对应点,点A和点B是对应点,下列结论中,错误的是( )
 如图所示,△ACF与△BDE全等,点A,B,C,D在同一条直线上,且点F和点E是对应点,点A和点B是对应点,下列结论中,错误的是( )
如图所示,△ACF与△BDE全等,点A,B,C,D在同一条直线上,且点F和点E是对应点,点A和点B是对应点,下列结论中,错误的是( )| A. | AF∥BE | B. | CF∥DE | C. | AB=CD | D. | ∠ACF=∠EBD |
16.雾霾已经成为现在生活中不得不面对的重要问题,PM2.5是大气中直径小于或等于0.000 002 5米的颗粒物,将0.000 002 5用科学记数法表示为( )
| A. | 2.5×10-6 | B. | 0.25×10-6 | C. | 2.5×10-5 | D. | 0.25×10-5 |
 如图,把一副三角板如图摆放,点E在边AC上,将图中的△ABC绕点A按每秒5°速度沿顺时针方向旋转一周,在旋转的过程中,在第21或57秒时,边BC恰好与边DE平行.
如图,把一副三角板如图摆放,点E在边AC上,将图中的△ABC绕点A按每秒5°速度沿顺时针方向旋转一周,在旋转的过程中,在第21或57秒时,边BC恰好与边DE平行.