题目内容
5.求下列函数中的自变量的取值范围.(1)y=$\frac{{x}^{2}-7x+3}{2}$;
(2)y=$\frac{{x}^{2}-x+1}{{x}^{2}-8x+15}$.
分析 根据分式的分母不能为零,可得答案.
解答 解:(1)x取任意实数y=$\frac{{x}^{2}-7x+3}{2}$都有意义,
y=$\frac{{x}^{2}-7x+3}{2}$的自变量的取值范围是x是全体实数;
(2)当x2-8x+15≠0时y=$\frac{{x}^{2}-x+1}{{x}^{2}-8x+15}$有意义,
解得x≠3,x≠3,
y=$\frac{{x}^{2}-x+1}{{x}^{2}-8x+15}$的取值范围是x≠3,x≠5.
点评 本题考查了函数自变量的取值范围,函数自变量的范围一般从三个方面考虑:当函数表达式是整式时,自变量可取全体实数;当函数表达式是分式时,考虑分式的分母不能为0;当函数表达式是二次根式时,被开方数非负.

练习册系列答案
相关题目
16.雾霾已经成为现在生活中不得不面对的重要问题,PM2.5是大气中直径小于或等于0.000 002 5米的颗粒物,将0.000 002 5用科学记数法表示为( )
| A. | 2.5×10-6 | B. | 0.25×10-6 | C. | 2.5×10-5 | D. | 0.25×10-5 |
13.化简:$\frac{\sqrt{2{5}^{2}-{7}^{2}}}{\sqrt{27}}$的结果是( )
| A. | $\frac{8\sqrt{6}}{3}$ | B. | $\frac{8\sqrt{3}}{9}$ | C. | $\frac{4\sqrt{6}}{3}$ | D. | $\frac{8\sqrt{3}}{3}$ |
 如图,将一副三角板的两个直角重合,使点B在EC上,点D在AC上,已知∠A=45°,∠E=30°,则∠BFD的度数是165°.
如图,将一副三角板的两个直角重合,使点B在EC上,点D在AC上,已知∠A=45°,∠E=30°,则∠BFD的度数是165°.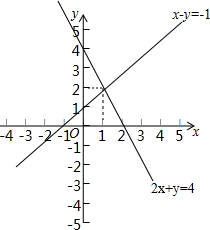 如图,在同一个平面直角坐标系中,画出二元一次方程组$\left\{{\begin{array}{l}{2x+y=4}\\{x-y=-1}\end{array}}\right.$中的两个二元一次方程的图象,由这两个二元一次方程的图象,可得出这个二元一次方程组的解是$\left\{\begin{array}{l}x=1\\ y=2\end{array}\right.$.
如图,在同一个平面直角坐标系中,画出二元一次方程组$\left\{{\begin{array}{l}{2x+y=4}\\{x-y=-1}\end{array}}\right.$中的两个二元一次方程的图象,由这两个二元一次方程的图象,可得出这个二元一次方程组的解是$\left\{\begin{array}{l}x=1\\ y=2\end{array}\right.$.