题目内容
3.(1)计算:|-3|-($\frac{1}{2}$)-2+20160;(2)若a=b+2,求代数式3a2-6ab+3b2的值.
分析 (1)直接利用绝对值的性质以及负整数指数幂的性质和零次方的性质化简求出答案;
(2)将原式分解因式,进而将已知代入求出答案.
解答 解:(1)|-3|-($\frac{1}{2}$)-2+20160
=3-4+1
=0;
(2)∵a=b+2,
∴a-b=2,
∴3a2-6ab+3b2
=3(a-b)2
=3×22
=12.
点评 此题主要考查了实数运算以及公式法分解因式,正确分解因式是解题关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
14.下列计算错误的有( )
①(2x+y)2=4x2+y2
②(-3b-a)(a-3b)=a2-9b2
③2×2-2=$\frac{1}{2}$
④(-1)0=-1
⑤(x-$\frac{1}{2}$)2=x2-2x+$\frac{1}{4}$
⑥(-a2)m=(-am)2.
①(2x+y)2=4x2+y2
②(-3b-a)(a-3b)=a2-9b2
③2×2-2=$\frac{1}{2}$
④(-1)0=-1
⑤(x-$\frac{1}{2}$)2=x2-2x+$\frac{1}{4}$
⑥(-a2)m=(-am)2.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
11.2022年将在北京-张家口举办冬季奥运会,很多学校开设了相关的课程.某校8名同学参加了冰壶选修课,他们被分成甲、乙两组进行训练,身高(单位:cm)如下表所示:
设两队队员身高的平均数依次为$\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$,方差依次为S甲2,S乙2,下列关系中完全正确的是( )
| 队员1 | 队员2 | 队员3 | 队员4 | |
| 甲组 | 176 | 177 | 175 | 176 |
| 乙组 | 178 | 175 | 177 | 174 |
| A. | $\overline{{x}_{甲}}=\overline{{x}_{乙}}$,S甲2<S乙2 | B. | $\overline{{x}_{甲}}=\overline{{x}_{乙}}$,S甲2>S乙2 | ||
| C. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,S甲2<S乙2 | D. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,S甲2>S乙2 |
18. 实数a,b在数轴上的对应点的位置如图所示,化简|a-b|的结果是( )
实数a,b在数轴上的对应点的位置如图所示,化简|a-b|的结果是( )
 实数a,b在数轴上的对应点的位置如图所示,化简|a-b|的结果是( )
实数a,b在数轴上的对应点的位置如图所示,化简|a-b|的结果是( )| A. | 0 | B. | a+b | C. | a-b | D. | b-a |
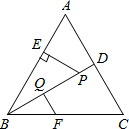 如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.若BF=2,求PE的长.
如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.若BF=2,求PE的长.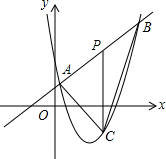 如图,直线y=x+4和抛物线y=ax2+bx+12(a≠0)相交于A(1,5)和B(8,n),点P是线段AB上异于A,B的动点,过点P作PC⊥x轴,交抛物线于点C.
如图,直线y=x+4和抛物线y=ax2+bx+12(a≠0)相交于A(1,5)和B(8,n),点P是线段AB上异于A,B的动点,过点P作PC⊥x轴,交抛物线于点C. 如图,在四边形ABCD中,AC⊥BD,EF∥AC∥HG,EH∥BD∥FG,求证:四边形EFGH是矩形.
如图,在四边形ABCD中,AC⊥BD,EF∥AC∥HG,EH∥BD∥FG,求证:四边形EFGH是矩形.