题目内容
8.已知二次根式$\sqrt{2{a}^{2}+1}$与$\sqrt{5}$是同类二次根式,试写出四个a的可能取值.分析 先根据同类二次根式的定义列出关于a的方程,求出a的可能值即可.
解答 解:∵二次根式$\sqrt{2{a}^{2}+1}$与$\sqrt{5}$是同类二次根式,
∴2a2+1=52n-1(n为大于等于1的整数),
当n=1时,2a2+1=5,解得a=±1;
当n=2时,2a2+1=125,解得a=±$\sqrt{62}$.
∴a可以是a=±1或a=±$\sqrt{62}$.
点评 本题考查的是同类二次根式,熟是一般地,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式是解答此题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
13.-$\frac{1}{8}$的立方根是( )
| A. | -$\frac{1}{2}$ | B. | $±\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{4}$ |
20.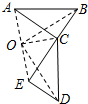 如图,△ABC绕着点O按顺时针方向旋转90°后到达了△CDE的位置,下列说法中不正确的是( )
如图,△ABC绕着点O按顺时针方向旋转90°后到达了△CDE的位置,下列说法中不正确的是( )
 如图,△ABC绕着点O按顺时针方向旋转90°后到达了△CDE的位置,下列说法中不正确的是( )
如图,△ABC绕着点O按顺时针方向旋转90°后到达了△CDE的位置,下列说法中不正确的是( )| A. | AB⊥CD | B. | AC⊥CE | ||
| C. | BC⊥DE | D. | 点C与点C是两个三角形的对应点 |
17.在多项式3x2y3z+4x5y2+6x4yz2中,各项的公因式是( )
| A. | x2yz | B. | 12x5y3z2 | C. | 12x2yz | D. | x2y |
 下面是从不同方向看用正方块塔建的几何体得到的平面图.
下面是从不同方向看用正方块塔建的几何体得到的平面图.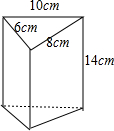 小明利用废纸板做一个三棱柱形无盖的笔筒,设计三棱柱立体模型如图所示,有关数据已标注在图上.
小明利用废纸板做一个三棱柱形无盖的笔筒,设计三棱柱立体模型如图所示,有关数据已标注在图上.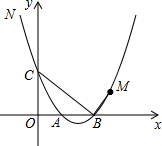 如图,抛物线y=$\frac{1}{2}$x2$-\frac{5}{2}$x+3与y轴交于点C,与x轴交于点A、B(A在B左侧),点M(4,m)在抛物线上,且在对称轴右侧,点N在抛物线上,△BMN是以BM为直角边的直角三角形,求N点坐标.
如图,抛物线y=$\frac{1}{2}$x2$-\frac{5}{2}$x+3与y轴交于点C,与x轴交于点A、B(A在B左侧),点M(4,m)在抛物线上,且在对称轴右侧,点N在抛物线上,△BMN是以BM为直角边的直角三角形,求N点坐标.