题目内容
17.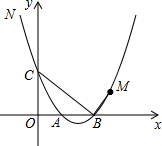 如图,抛物线y=$\frac{1}{2}$x2$-\frac{5}{2}$x+3与y轴交于点C,与x轴交于点A、B(A在B左侧),点M(4,m)在抛物线上,且在对称轴右侧,点N在抛物线上,△BMN是以BM为直角边的直角三角形,求N点坐标.
如图,抛物线y=$\frac{1}{2}$x2$-\frac{5}{2}$x+3与y轴交于点C,与x轴交于点A、B(A在B左侧),点M(4,m)在抛物线上,且在对称轴右侧,点N在抛物线上,△BMN是以BM为直角边的直角三角形,求N点坐标.
分析 首先求得M的坐标,以及A和B的坐标,利用待定系数法求得BM的解析式,然后分成B是直角顶点和M是直角顶点两种情况进行讨论,求得另一直角边的解析式,从而求得N的坐标.
解答 解:在y=$\frac{1}{2}$x2$-\frac{5}{2}$x+3中令x=4,则y=8-10+3=1,
则M的坐标是(4,1).
在y=$\frac{1}{2}$x2$-\frac{5}{2}$x+3中令y=0,则$\frac{1}{2}$x2-$\frac{5}{2}$x+3=0,解得:x=2或3,
则B的坐标是(3,0).
设BM的解析式是y=kx+b,
根据题意得:$\left\{\begin{array}{l}{3k+b=0}\\{4k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$,
则直线BM的解析式是y=x-3.
设经过M且垂直于BM的直线的解析式是y=-x+c,
把(4,1)代入得-4+c=1,解得:c=5,
则解析式是y=-x+5.
根据题意得$\frac{1}{2}$x2$-\frac{5}{2}$x+3=-x+5,
即x2-3x-4=0,
解得:x=-1或4,
则N的横坐标是-1,把x=-1代入y=$\frac{1}{2}$x2$-\frac{5}{2}$x+3=6,则N的坐标是(-1,6);
设经过B且垂直于BM的直线的解析式是y=-x+d,
把(3,0)代入得-3+c=0,解得:c=3,
则解析式是y=-x+3.
根据题意得$\frac{1}{2}$x2$-\frac{5}{2}$x+3=-x+3,
解得:x=0或3.
当x=0时,y=3,则此时N的坐标是(0,3).
总之,N的坐标是(-1,6)或(0,3).
点评 本题考查了待定系数法求函数的解析式,以及一次函数的图象互相垂直的关系,求得另一直角边的解析式是本题的关键.

 初中暑期衔接系列答案
初中暑期衔接系列答案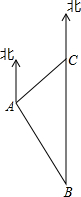 海上有两个灯塔B,C,其中灯塔C位于灯塔B的正北方向20海里处,在点A处测得灯塔C位于A的东北方向上,A位于灯塔B的北偏西30°方向上,点A与灯塔C之间的距离是多少?(结果精确到0.1海里.参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
海上有两个灯塔B,C,其中灯塔C位于灯塔B的正北方向20海里处,在点A处测得灯塔C位于A的东北方向上,A位于灯塔B的北偏西30°方向上,点A与灯塔C之间的距离是多少?(结果精确到0.1海里.参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73) 一个几何体是由若干个相同的小立方块搭成的,它的主视图和左视图相同,如图所示,搭成该几何体的小立方块最多几块?最少几块?画出相应的俯视图,并在俯视图上用数字表示该位置小立方块的个数.
一个几何体是由若干个相同的小立方块搭成的,它的主视图和左视图相同,如图所示,搭成该几何体的小立方块最多几块?最少几块?画出相应的俯视图,并在俯视图上用数字表示该位置小立方块的个数.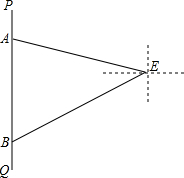 如图,灯塔E到一段南北向航线PQ的距离为10海里,一艘船沿此航线由北向南航行,在点A在灯塔E的北偏西68°方向,点B处在灯塔E西南方向,求轮AB的距离(精确到0.1海里/时).
如图,灯塔E到一段南北向航线PQ的距离为10海里,一艘船沿此航线由北向南航行,在点A在灯塔E的北偏西68°方向,点B处在灯塔E西南方向,求轮AB的距离(精确到0.1海里/时).