Question

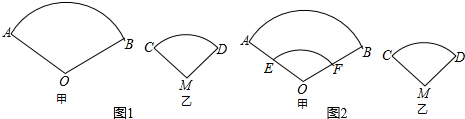
3．如图1，两个扇形纸扇的圆心角都是120°，OA=2MD=40cm．
（1）扇形两面都贴纸，分别求图1中两个扇形所用纸的面积是多少．（π取3）
（2）如图2，OE=20cm．若扇形AOB中的小扇形EOF部分（阴影部分）不贴纸，试比较哪个扇形用纸面较大．（π取3）
（3）若甲扇形的半径是乙扇形半径的2倍，圆心角是乙扇形圆心角的一半，则甲扇形的面积是乙扇形面积的2倍．

Answer 1

分析 （1）只需运用扇形的面积公式就可解决问题；
（2）只需运用（1）中的结果就可算出两个扇形用纸面积，通过比较就可解决问题；
（3）设乙扇形半径为r，圆心角为α，则甲扇形的半径为2r，圆心角为$\frac{1}{2}$α，然后只需运用扇形的面积公式就可解决问题．

解答 解：（1）如图1，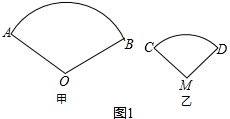

甲扇形所用纸的面积为2×$\frac{120π•O{A}^{2}}{360}$=2×$\frac{120×3×4{0}^{2}}{360}$=3200，
乙扇形所用纸的面积为2×$\frac{120πM{D}^{2}}{360}$=2×$\frac{120×3×2{0}^{2}}{360}$=800；
（2）如图2，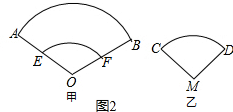

甲扇形所用纸的面积为3200-800=2400，乙扇形所用纸的面积为800，
∴甲扇形用纸面较大；

（3）设乙扇形半径为r，圆心角为α，则甲扇形的半径为2r，圆心角为$\frac{1}{2}$α，
∴S_甲扇形=$\frac{\frac{1}{2}απ（2r）^{2}}{360}$=$\frac{πα{r}^{2}}{180}$，S_乙扇形=$\frac{α•π•{r}^{2}}{360}$，
∴S_甲扇形=2S_乙扇形．
故答案为2．

点评 本题考查的是扇形面积公式的运用，其中半径为r，圆心角为n°的扇形的面积为$\frac{nπ{r}^{2}}{360}$；需要注意的是（1）中扇形两面都贴纸，扇形所用纸的面积应是扇形面积的2倍．