题目内容
下列事件发生的可能性为0的是( )
A. 掷两枚骰子,同时出现数字“6”朝上
B. 小明从家里到学校用了10分钟,从学校回到家里却用了15分钟
C. 今天是星期天,昨天必定是星期六
D. 小明步行的速度是每小时40千米
 D
【解析】对于A,掷两枚骰子,同时出现数字“6”朝上,可能性为;
对于B,小明从家里到学校用了10分钟,从学校回到家里却用了15分钟是可能是,比如去学校时下坡,则回家时上坡,当然回家比去学校用时多;
对于C,今天是星期天,昨天必定是星期六这是一个必然发生的事件,可能性为1;
对于D,小明步行的速度是每小时40千米,是不存在的.一般人步行的速度为3-5公里每小时,所以D发生...
D
【解析】对于A,掷两枚骰子,同时出现数字“6”朝上,可能性为;
对于B,小明从家里到学校用了10分钟,从学校回到家里却用了15分钟是可能是,比如去学校时下坡,则回家时上坡,当然回家比去学校用时多;
对于C,今天是星期天,昨天必定是星期六这是一个必然发生的事件,可能性为1;
对于D,小明步行的速度是每小时40千米,是不存在的.一般人步行的速度为3-5公里每小时,所以D发生...
练习册系列答案
相关题目
已知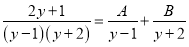 ,求A、B的值.
,求A、B的值.
 A=1,B=1.
【解析】试题分析:已知等式右边两项通分并利用同分母分式的加法法则计算,利用分式相等的条件即可求出A与B.
试题解析:
【解析】
===,
∴,
解得: .
A=1,B=1.
【解析】试题分析:已知等式右边两项通分并利用同分母分式的加法法则计算,利用分式相等的条件即可求出A与B.
试题解析:
【解析】
===,
∴,
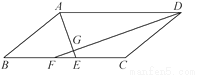
解得: . 已知:如图,在?ABCD中,∠ADC,∠DAB的平分线DF,AE分别与线段BC相交于点F,E,DF与AE相交于点G.
(1)求证:AE⊥DF;
(2)若AD=10,AB=6,AE=4,求DF的长.
 (1)证明见解析;(2).
【解析】试题分析:(1)根据平行四边形的性质和平行线的性质推出∠ADC+∠DAB=180°,根据角平分线得到∠ADF+∠DAE=(∠ADC+∠DAB)=90°,即可求出结论;
(2)过点D作DH∥AE,交BC的延长线于点H,得到平行四边形AEHD,求出DH=AE=4,EH=AD=10,根据平行四边形的性质和平行线的性质推出DC=FC,AB=EB,求出BF、F...
(1)证明见解析;(2).
【解析】试题分析:(1)根据平行四边形的性质和平行线的性质推出∠ADC+∠DAB=180°,根据角平分线得到∠ADF+∠DAE=(∠ADC+∠DAB)=90°,即可求出结论;
(2)过点D作DH∥AE,交BC的延长线于点H,得到平行四边形AEHD,求出DH=AE=4,EH=AD=10,根据平行四边形的性质和平行线的性质推出DC=FC,AB=EB,求出BF、F... 为了了解参加某运动会的2000名运动员的年龄情况,从中抽查了100名运动员的年龄,“某运动员被抽到”这一事件是______事件.
 随机.
【解析】由题意知是从2000名运动员的年龄中抽取100名运动员的年龄,每一名运动员被投到的频率为,即为,所以某运动员被抽到这一事件是随机事件.
随机.
【解析】由题意知是从2000名运动员的年龄中抽取100名运动员的年龄,每一名运动员被投到的频率为,即为,所以某运动员被抽到这一事件是随机事件. 下列事件中,随机事件是( )
A. 没有水分,种子仍能发芽 B. 等腰三角形两个底角相等
C. 从13张红桃扑克牌中任抽一张,是红桃A D. 从13张方块扑克牌中任抽一张,是红桃10
 C
【解析】对于A,没有水分,种子仍能发芽,这是一个不可能事件,发生的可能性为0;对于B,是一个必然事件,发生的可能性是1;对于C,是一个随机事件,发生的可能性是;对于D,是一个不可能事件,发生的可能性是0.发生的可能性是0和1的,都属于必然事件.
故选C.
C
【解析】对于A,没有水分,种子仍能发芽,这是一个不可能事件,发生的可能性为0;对于B,是一个必然事件,发生的可能性是1;对于C,是一个随机事件,发生的可能性是;对于D,是一个不可能事件,发生的可能性是0.发生的可能性是0和1的,都属于必然事件.
故选C. 下列条形中的能代圆形图所表示的数据( )

A. 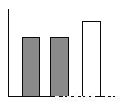 B.
B. 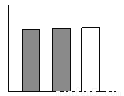 C.
C. 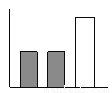 D.
D. 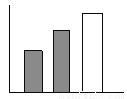
 C
【解析】由图知,阴影部分与空白部分面积相等,在给出的四个选项中,只有C中有阴影的两个矩形面积之和等于空白矩形面积.
故选C.
C
【解析】由图知,阴影部分与空白部分面积相等,在给出的四个选项中,只有C中有阴影的两个矩形面积之和等于空白矩形面积.
故选C. 如图所示,已知在平行四边形ABCD中,BE=DF.求证:AE=CF.
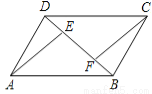
 证明:∵BE=DF,
∴BE-EF=DF-EF,
∴DE=BF,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS),
∴AE=CF.
【解析】
求出DE=BF,根据平行四边形性质求出AD=BC,AD∥BC,推出∠ADE=∠CBF,证出△ADE≌△CBF即可.
证明:∵BE=DF,
∴BE-EF=DF-EF,
∴DE=BF,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS),
∴AE=CF.
【解析】
求出DE=BF,根据平行四边形性质求出AD=BC,AD∥BC,推出∠ADE=∠CBF,证出△ADE≌△CBF即可. 如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是________.
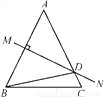
 50°
【解析】根据线段垂直平分线上的点到两端点的距离相等可得AD=BD,根据等边对等角可得∠A=∠ABD,然后表示出∠ABC,再根据等腰三角形两底角相等可得∠C=∠ABC,然后根据三角形的内角和定理列出方程求解即可.
【解析】
∵MN是AB的垂直平分线,
∴AD=BD,
∴∠A=∠ABD,
∵∠DBC=15°,
∴∠ABC=∠A+15°,
∵AB=AC...
50°
【解析】根据线段垂直平分线上的点到两端点的距离相等可得AD=BD,根据等边对等角可得∠A=∠ABD,然后表示出∠ABC,再根据等腰三角形两底角相等可得∠C=∠ABC,然后根据三角形的内角和定理列出方程求解即可.
【解析】
∵MN是AB的垂直平分线,
∴AD=BD,
∴∠A=∠ABD,
∵∠DBC=15°,
∴∠ABC=∠A+15°,
∵AB=AC... 分解因式:①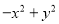 =____________ ;②
=____________ ;②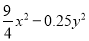 =_________________.
=_________________.
 ;
【解析】①=y2-x2=(y+x)(y-x);
②= (9x2-y2)= (3x+y)(3x-y),
故答案为:①;② .
;
【解析】①=y2-x2=(y+x)(y-x);
②= (9x2-y2)= (3x+y)(3x-y),
故答案为:①;② . 
