题目内容
1.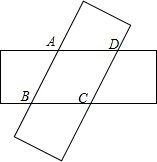 如图,由两个长为10,宽为2的矩形叠合而得到菱形ABCD,则菱形ABCD面积的最大值为$\frac{52}{5}$.
如图,由两个长为10,宽为2的矩形叠合而得到菱形ABCD,则菱形ABCD面积的最大值为$\frac{52}{5}$.
分析 菱形的一条对角线为矩形的对角线时,面积最大,作出图形,设边长为x,表示出BE=10-x,再利用勾股定理列式计算求出x,然后根据菱形的四条边都相等列式进行计算即可得解出边长,再计算面积即可.
解答 解: 如图,菱形的一条对角线与矩形的对角线重合时,面积最大,
如图,菱形的一条对角线与矩形的对角线重合时,面积最大,
设AB=BC=x,则BE=10-x,
在Rt△BCE中,BC2=BE2+CE2,
即x2=(10-x)2+22,
解得x=$\frac{26}{5}$,
所以S菱形ABCD=$\frac{26}{5}$×2=$\frac{52}{5}$.
故答案为:$\frac{52}{5}$.
点评 本题考查了菱形的性质,勾股定理的应用,主要利用了菱形的四条边都相等的性质,判断出面积最小与最大时的情况是解题的关键,作出图形更形象直观.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列各数中 $0.\stackrel{•}3\stackrel{•}2$、π、$-\sqrt{3}$、0、0.1010010001…(相邻两个1之间0的个数逐次加1)、$\frac{7}{11}$、$\root{3}{27}$、-8、$\sqrt{1.44}$,无理数的个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
11.若关于x的一元二次方程(a-2)x2-4x-1=0有实数根,则a满足( )
| A. | a≥-2 | B. | a>-2且a≠2 | C. | a≥-2且a≠2 | D. | a≠2 |
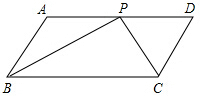 如图,在平行四边形ABCD中,P是AD上的一点,且BP和CP分别平分∠ABC和∠BCD.
如图,在平行四边形ABCD中,P是AD上的一点,且BP和CP分别平分∠ABC和∠BCD.