题目内容
10.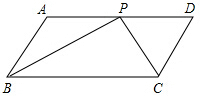 如图,在平行四边形ABCD中,P是AD上的一点,且BP和CP分别平分∠ABC和∠BCD.
如图,在平行四边形ABCD中,P是AD上的一点,且BP和CP分别平分∠ABC和∠BCD.(1)求∠BPC的度数;
(2)如果AB=5cm,BP=8cm,求三角形BPC的面积.
分析 (1)根据平行四边形的同旁内角互补,再结合角平分线的定义,可以得到∠PAB+∠PBA=90°,再根据三角形的内角和定理就可证明;
(2)根据角平分线的定义以及两条直线平行,则内错角相等.从而证明△ABP和△CDP是等腰三角形.则AD=CB=PD+AP=10,根据勾股定理得到PC=6,再根据直角三角形的面积等于两条直角边的乘积的一半.
解答 (1)证明:∵BP和CP分别平分∠ABC和∠BCD,
∴∠PBC=$\frac{1}{2}$∠ABC,∠PCB=$\frac{1}{2}∠$DCB,
又∵四边形ABCD是平行四边形,
∴AB∥BD,
∴∠ABC+∠DCB=180°
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠DCB)=90°,
∴∠BPC=180°-90°=90°;
(2)解:∵四边形ABCD是平行四边形,
∴CD=AB=5,AD∥BC,
∴∠APB=∠PBC,
又∵BP和CP分别平分∠ABC和∠BCD,
∴∠PAB=∠PAD=∠DPA,
∴AP=AB=5,
同理PD=CD=5,
∴AD=BC=AP+PD=10,
∴在Rt△BPC中,由勾股定理得:PC=$\sqrt{B{C}^{2}-B{P}^{2}}$=6.
∴S△BPC=$\frac{1}{2}$BP•PC=24.
点评 本题考查了平行四边形性质,平行线性质,等腰三角形的性质和判定,三角形的内角和定理,勾股定理等知识点的综合运用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
20.在实数$\root{3}{-27}$,0.101 001 0001,π,$\sqrt{5}$中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.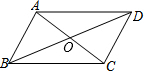 如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
 如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )| A. | 当∠ABC=90°时,它是矩形 | B. | 当AO=CO,BO=DO时,它是菱形 | ||
| C. | 当AC⊥BD时,它是菱形 | D. | 当AC=BD且AC⊥BD时,它是正方形 |
2.若关于x的方程$\frac{x+2}{x-1}=\frac{m+1}{x-1}$产生增根,则m是( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
19.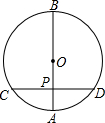 如图,在⊙O中,直径AB垂直于弦CD,垂足为P.若PA=2,PB=8,则CD的长为( )
如图,在⊙O中,直径AB垂直于弦CD,垂足为P.若PA=2,PB=8,则CD的长为( )
 如图,在⊙O中,直径AB垂直于弦CD,垂足为P.若PA=2,PB=8,则CD的长为( )
如图,在⊙O中,直径AB垂直于弦CD,垂足为P.若PA=2,PB=8,则CD的长为( )| A. | 2$\sqrt{5}$ | B. | 4 | C. | 8 | D. | $4\sqrt{5}$ |
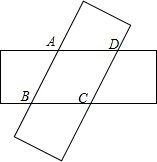 如图,由两个长为10,宽为2的矩形叠合而得到菱形ABCD,则菱形ABCD面积的最大值为$\frac{52}{5}$.
如图,由两个长为10,宽为2的矩形叠合而得到菱形ABCD,则菱形ABCD面积的最大值为$\frac{52}{5}$.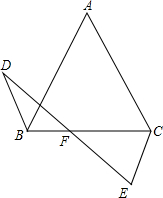 如图所示,△ABC中,AB=AC,点D在△ABC的外部,且∠ABD是锐角,点E在射线AC的左侧,且∠ACE与∠ABD互补,BD=CE,DE与BC相交于点F.
如图所示,△ABC中,AB=AC,点D在△ABC的外部,且∠ABD是锐角,点E在射线AC的左侧,且∠ACE与∠ABD互补,BD=CE,DE与BC相交于点F. 如图,点Q在直线y=-x上运动,点A的坐标为(3,0),点B的坐标为(0,2),当AQ+BQ最短时,点Q的坐标为(0,0).
如图,点Q在直线y=-x上运动,点A的坐标为(3,0),点B的坐标为(0,2),当AQ+BQ最短时,点Q的坐标为(0,0).