下列各数中 $0.\stackrel{•}3\stackrel{•}2$.π.$-\sqrt{3}$.0.0.1010010001-(相邻两个1之间0的个数逐次加1).$\frac{7}{11}$.$\root{3}{27}$.-8.$\sqrt{1.44}$.无理数的个数为( )A．2个B．3个C．4个D．5个题目和参考答案——青夏教育精英家教网—

题目内容

12．下列各数中 $0.\stackrel{•}3\stackrel{•}2$、π、$-\sqrt{3}$、0、0.1010010001…（相邻两个1之间0的个数逐次加1）、$\frac{7}{11}$、$\root{3}{27}$、-8、$\sqrt{1.44}$，无理数的个数为（　　）

A．

2个

B．

3个

C．

4个

D．

5个

分析根据无理数的三种形式求解．

解答解：$\root{3}{27}$=3，$\sqrt{1.44}$=1.2，
无理数为：π、$-\sqrt{3}$、0、0.1010010001…，共3个．
故选B．

点评本题考查了无理数的知识，解答本题的关键是掌握无理数的三种形式：①开方开不尽的数，②无限不循环小数，③含有π的数．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

3．用配方法解方程：2x²+2x-1=0．

20．在实数$\root{3}{-27}$，0.101 001 0001，π，$\sqrt{5}$中，无理数有（　　）

7．

如图，在△ABC中，D，E，F分别为BC，AC，AB边的中点，AH⊥BC于H，FD=8，则HE等于（　　）

17．

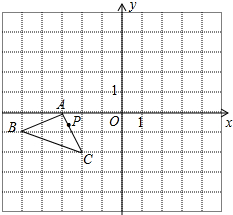如图，在平面直角坐标系中，P（a，b）是△ABC的边AC上一点，△ABC经平移后点P的对应点为P₁（a+5，b+4）
（1）请画出上述平移后的△A₁B₁C₁；
（2）写出A₁，B₁，C₁三个点的坐标；
（3）求△ABC的面积．

4．三峡大坝下闸蓄水，最初库区有一定数量的垃圾，另外，蓄水过程中每天都有新的定量垃圾流到大坝库区，为了保证大坝正常工作，必须边蓄水边打捞清除垃圾．按当时的垃圾流入量，40天可打捞完毕．蓄水后，前5天上游降雨，江水猛涨，每天的垃圾流入量比原来增加20%，而打捞量不变．这时，经有关部门测算：如果其后的垃圾流入量仍和原来一样，而打捞量增加10%，则再用30天可打捞完毕；如果其后每天垃圾流入量变成原来的k倍，而打捞量增加10%，则从这时起20天后，库区垃圾正好是最初的一半．
（1）求出原来每天的打捞量与原来每天的垃圾流入量的比值；
（2）求k的值．

1．

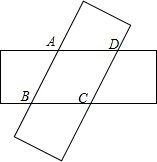如图，由两个长为10，宽为2的矩形叠合而得到菱形ABCD，则菱形ABCD面积的最大值为$\frac{52}{5}$．

2．若关于x的方程$\frac{x+2}{x-1}=\frac{m+1}{x-1}$产生增根，则m是（　　）

试题分类