题目内容
19.把$\frac{\sqrt{a}}{\sqrt{b}}$=$\sqrt{\frac{a}{b}}$反过来就可以进行二次根式的化简.$\sqrt{\frac{a}{b}}$=$\frac{\sqrt{(\;\;\;\;)}}{\sqrt{(\;\;\;\;)}}$(a≥0,b>0)
(1)$\sqrt{\frac{3}{100}}$=$\frac{\sqrt{3}}{10}$;(2)$\sqrt{\frac{75}{27}}$=$\frac{5}{3}$.
分析 根据二次根式的性质,即可解答;
(1)根据所给的例子,解析解答即可;
(2)根据所给的例子,解析解答即可.
解答 解:$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}(a≥0,b>0)$,
(1)$\sqrt{\frac{3}{100}}=\frac{\sqrt{3}}{\sqrt{100}}=\frac{\sqrt{3}}{10}$,
(2)$\sqrt{\frac{75}{27}}=\frac{\sqrt{75}}{\sqrt{27}}=\frac{5\sqrt{3}}{3\sqrt{3}}=\frac{5}{3}$,
故答案为:b,$\frac{\sqrt{3}}{10}$,$\frac{5}{3}$.
点评 本题二次根式的性质,解决本题的关键是熟记二次根式的性质.

练习册系列答案
相关题目
7. 如图,已知∠1=60°,如果CD∥BE,那么∠B的度数为( )
如图,已知∠1=60°,如果CD∥BE,那么∠B的度数为( )
 如图,已知∠1=60°,如果CD∥BE,那么∠B的度数为( )
如图,已知∠1=60°,如果CD∥BE,那么∠B的度数为( )| A. | 60° | B. | 100° | C. | 110 | D. | 120° |
11.已知代数式$\frac{1}{2}$xa-1y3与-3xby2a-b是同类项,那么a,b的值分别是( )
| A. | $\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=-2}\\{b=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-2}\\{b=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$ |
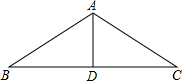 如图,已知房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC,求顶架上∠B、∠C、∠BAD、∠CAD的度数.
如图,已知房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC,求顶架上∠B、∠C、∠BAD、∠CAD的度数.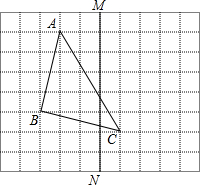 如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上.
如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上.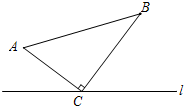 如图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点M从A点出发沿A→C→B路径向终点运动,终点为B点,点N从B点出发沿B→C→A路径向终点运动,终点为A点,点M和N分别以每秒2m和3cm的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作ME⊥l于E,NF⊥l于F.设运动时间为t秒,要使以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等,则t的值为$\frac{23}{5}$或7或8.
如图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点M从A点出发沿A→C→B路径向终点运动,终点为B点,点N从B点出发沿B→C→A路径向终点运动,终点为A点,点M和N分别以每秒2m和3cm的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作ME⊥l于E,NF⊥l于F.设运动时间为t秒,要使以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等,则t的值为$\frac{23}{5}$或7或8.