题目内容
9.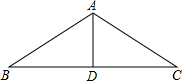 如图,已知房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC,求顶架上∠B、∠C、∠BAD、∠CAD的度数.
如图,已知房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC,求顶架上∠B、∠C、∠BAD、∠CAD的度数.
分析 先根据等腰三角形的性质得出∠B=∠C,再由三角形内角和定理即可求出∠B的度数,根据等腰三角形三线合一的性质即可求出∠BAD的度数.
解答 解:∵△ABC中,AB=AC,∠BAC=100°,
∴∠B=∠C=$\frac{180°-∠BAC}{2}$=$\frac{180°-100°}{2}$=40°;
∵AB=AC,AD⊥BC,∠BAC=100°,
∴AD平分∠BAC,
∴∠BAD=∠CAD=50°.
点评 本题考查的是等腰三角形的性质及三角形的内角和定理,熟记等腰三角形的性质-三线合一是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.如图是小李书桌上放的一本书,则这本书的俯视图是( )


| A. |  | B. |  | C. |  | D. |  |
 如图,在平行四边形ABCD中,AM⊥BD于M,CN⊥BD于N,连接CM、AN
如图,在平行四边形ABCD中,AM⊥BD于M,CN⊥BD于N,连接CM、AN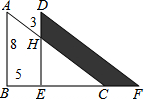 如图,原来是重叠的两个直角三角形,将其中一个三角形沿着BC方向平移线段BE的距离,就得到此图形,下列结论正确的有( )
如图,原来是重叠的两个直角三角形,将其中一个三角形沿着BC方向平移线段BE的距离,就得到此图形,下列结论正确的有( )