题目内容
7.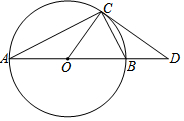 如图,已知:AB是⊙O的直径,点C是⊙O上的一点,切线CD交AB的延长线于D.
如图,已知:AB是⊙O的直径,点C是⊙O上的一点,切线CD交AB的延长线于D.(1)求证:△CBD∽△ACD.
(2)若CD=4,BD=2,求直径AB的长.
(3)在(2)的前提下求tan∠CAB的值.
分析 (1)由AB为直径得到∠ACO+∠BCO=90°,利用切线的性质得∠BCO+∠BCD=90°,则根据等角的余角相等得到∠BCD=∠ACO,加上∠ACO=∠A,则∠A=∠BCD,则可根据相似三角形的判定方法可得到结论;
(2)由△CBD∽△ACD得到DC:DA=DB:DC,然后利用比例性质可求出AB;
(3)由△CBD∽△ACD得到$\frac{BC}{AC}$=$\frac{BD}{CD}$=$\frac{2}{4}$=$\frac{1}{2}$,然后根据正切的定义求解.
解答 (1)证明:∵AB为直径,
∴∠ACB=90°,即∠ACO+∠BCO=90°,
∵CD为切线,
∴OC⊥CD,
∴∠BCO+∠BCD=90°,
∴∠BCD=∠ACO,
∵OA=OC,
∴∠ACO=∠A,
∴∠A=∠BCD,
而∠BDC=∠CDA,
∴△CBD∽△ACD;
(2)解:∵△CBD∽△ACD,
∴DC:DA=DB:DC,即4:(2+AB)=2:4,
∴AB=6;
(3)解:∵△CBD∽△ACD,
∴$\frac{BC}{AC}$=$\frac{BD}{CD}$=$\frac{2}{4}$=$\frac{1}{2}$,
在Rt△ABC中,tan∠CAB=$\frac{BC}{AC}$=$\frac{1}{2}$.
点评 本题考查了三角形相似的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;在运用相似三角形的性质时,主要利用相似进行几何计算.也考查了切线的性质.

练习册系列答案
相关题目
19.若单项式-2xm-1ymn与7x3y2是同类项,则代数式m-n的值是( )
| A. | -$\frac{7}{2}$ | B. | 2 | C. | $\frac{7}{2}$ | D. | -2 |
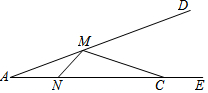 如图,已知∠DAE=22.5°,点C是射线AE上一点,且线段AC=3,若点M和点N分别是射线AD和线段AC上的两个动点,则MN+MC的最小值是$\frac{3\sqrt{2}}{2}$.
如图,已知∠DAE=22.5°,点C是射线AE上一点,且线段AC=3,若点M和点N分别是射线AD和线段AC上的两个动点,则MN+MC的最小值是$\frac{3\sqrt{2}}{2}$.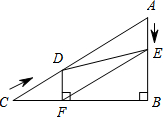 如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.
如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.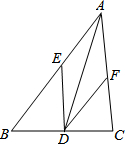 如图,已知AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.
如图,已知AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.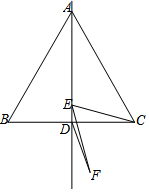 如图,已知等边△ABC边长为8 cm,D为BC中点,E为直线AD上一动点,将EC绕着点E顺时针旋转60°得到线段EF,连接DF,则线段DF最小值为2.
如图,已知等边△ABC边长为8 cm,D为BC中点,E为直线AD上一动点,将EC绕着点E顺时针旋转60°得到线段EF,连接DF,则线段DF最小值为2.