题目内容
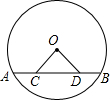如图，AB是⊙O的弦，点C、D在弦AB上，且AD=BC，联结OC、OD．求证：△OCD是等腰三角形．考点：垂径定理,等腰三角形的判定
专题：证明题
分析：过O作OE⊥AB于E，根据垂径定理求出AE=BE，求出CE=DE，根据线段垂直平分线性质求出OD=OC，即可得出答案．
解答：证明：
过O作OE⊥AB于E，
则AE=BE，
∵AD=BC，
∴AD-DC=BC-DC，
∴AC=DE，
∴CE=DE，
∵OE⊥CD，
∴OC=OD，
即△OCD是等腰三角形．
过O作OE⊥AB于E，
则AE=BE，
∵AD=BC，
∴AD-DC=BC-DC，
∴AC=DE，
∴CE=DE，
∵OE⊥CD，
∴OC=OD，
即△OCD是等腰三角形．
点评：本题考查了垂径定理，等腰三角形的判定，线段垂直平分线性质的应用，解此题的关键是正确作出辅助线后求出CE=DE．
练习册系列答案
阅读快车系列答案
相关题目
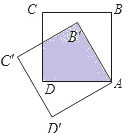如图，正方形ABCD绕点A逆时针旋转，得到正方形AB′C′D′，当两正方形重叠部分的面积是原正方形面积的在Rt△ABC中，已知∠C=90°，AC=3，BC=4，那么∠A的余弦值等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
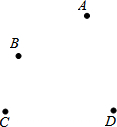如图，平面上四个点A，B，C，D．按要求完成下列问题：
抛物线y=ax2+bx+c（a≠0）向右平移2个单位得到抛物线y=a（x-3）2-1，且平移后的抛物线经过点A（2，1）．
