题目内容
在Rt△ABC中,∠C=90°,∠A=30°,BC=1,分别以A、B为圆心的两圆外切,如果点C在圆A内,那么圆B的半径长r的取值范围是 .
考点:点与圆的位置关系
专题:
分析:首先根据题意求得斜边AB和直角边AC的长,要使得点C在圆A内圆A的半径就满足比AC长、比AB短,从而得解.
解答:解:∵Rt△ABC中,∠C=90°,∠A=30°,BC=1,
∴AB=2BC=2,AC=
=
,
∵以A、B为圆心的两圆外切,
∴两圆的半径的和为2,
∵点C在圆A内,
∴圆A的半径长r的取值范围是0<r<2-
,
故答案为:0<r<2-
.
∴AB=2BC=2,AC=
| 22-12 |
| 3 |
∵以A、B为圆心的两圆外切,
∴两圆的半径的和为2,
∵点C在圆A内,
∴圆A的半径长r的取值范围是0<r<2-
| 3 |
故答案为:0<r<2-
| 3 |
点评:考查了点与圆的位置关系,判断点与圆的位置关系,也就是比较点与圆心的距离和半径的大小关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
A、B、C三点分别表示家、学校、超市,若学校在家的南偏西78°方向,超市在家的北偏东24°方向,则∠BAC的度数为( )
| A、102° | B、126° |
| C、132° | D、123° |
已知
=
,那么下列等式中,不一定正确的是( )
| a |
| b |
| 5 |
| 2 |
| A、2a=5b | ||||
B、
| ||||
| C、a+b=7 | ||||
D、
|

 如图,在△ABC中,D是BC边上一点,BD=m,CD=n,则
如图,在△ABC中,D是BC边上一点,BD=m,CD=n,则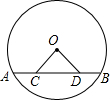 如图,AB是⊙O的弦,点C、D在弦AB上,且AD=BC,联结OC、OD.求证:△OCD是等腰三角形.
如图,AB是⊙O的弦,点C、D在弦AB上,且AD=BC,联结OC、OD.求证:△OCD是等腰三角形. 如图,三角板ABC中,∠ACB=90°,∠B=30°,AC=2
如图,三角板ABC中,∠ACB=90°,∠B=30°,AC=2