题目内容
已知四边形ABCD内接于⊙O,对角线AC,BD交于点P.
(1)如图1,设⊙O的半径是r,若
+
=πr,求证:AC⊥BD;
(2)如图2,过点A作AE⊥BC,垂足为G,AE交BD于点M,交⊙O于点E;过点D作DH⊥BC,垂足为H,DH交AC于点N,交⊙O于点F;若AC⊥BD,求证:MN=EF.

(1)如图1,设⊙O的半径是r,若
 |
| AB |
 |
| CD |
(2)如图2,过点A作AE⊥BC,垂足为G,AE交BD于点M,交⊙O于点E;过点D作DH⊥BC,垂足为H,DH交AC于点N,交⊙O于点F;若AC⊥BD,求证:MN=EF.

考点:圆的综合题
专题:
分析:(1)连接AO,BO,CO,DO设∠AOB=m°,∠DOC=n°,利用
+
=πr,得出m+n=180,再利用圆周角与圆心角的关系求出∠APD=90°,即可得出AC⊥BD;
(2)由DH⊥BC,AE⊥BC,可得出DF∥AE,进而得出∠AEF+∠DFE=180°结合四边形ABCD内接于⊙O,可得出∠AEF=∠DAE,从而得出四边形DAEF为等腰梯形,得出AD=EF,再由角的关系得出AD=AM,PD=PM,易证△NDP≌△AMP,得出ND=AM,所以四边形AMND是平行四边形,再由MN=AD,即可得出MN=EF.
 |
| AB |
 |
| CD |
(2)由DH⊥BC,AE⊥BC,可得出DF∥AE,进而得出∠AEF+∠DFE=180°结合四边形ABCD内接于⊙O,可得出∠AEF=∠DAE,从而得出四边形DAEF为等腰梯形,得出AD=EF,再由角的关系得出AD=AM,PD=PM,易证△NDP≌△AMP,得出ND=AM,所以四边形AMND是平行四边形,再由MN=AD,即可得出MN=EF.
解答:证明:(1)如图1,连接AO,BO,CO,DO设∠AOB=m°,∠DOC=n°,
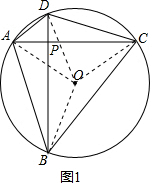
∵
+
=πr,
∴
+
=πr,
∴m+n=180,
∴2∠ADB+2∠DAC=180°
∴∠ADB+∠DAC=90°,
∴∠APD=90°,
∴AC⊥BD,
(2)如图2,
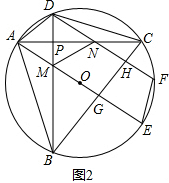
∵DH⊥BC,AE⊥BC,
∴DF∥AE,
∴∠AEF+∠DFE=180°
∵四边形ABCD内接于⊙O,
∴∠DAE+∠DFE=180°,
∴∠AEF=∠DAE,
∴四边形DAEF为等腰梯形,
∴AD=EF,
∵AC⊥BD,
∴∠PAM+∠AMP=90°,
AG⊥BC,
∴∠PAM+∠ACB=90°,
∴∠AMP=∠ACB,
∵∠ADB=∠ACB,
∴∠ADB=∠AMP,
∴AD=AM,
∴PD=PM,
∵DF∥AE,
∴∠AMP=∠NDP
∴△NDP≌△AMP,
∴ND=AM,
∴四边形AMND是平行四边形,
∴MN=AD,
∴MN=EF.

∵
 |
| AB |
 |
| CD |
∴
| mπr |
| 180 |
| nπr |
| 180 |
∴m+n=180,
∴2∠ADB+2∠DAC=180°
∴∠ADB+∠DAC=90°,
∴∠APD=90°,
∴AC⊥BD,
(2)如图2,

∵DH⊥BC,AE⊥BC,
∴DF∥AE,
∴∠AEF+∠DFE=180°
∵四边形ABCD内接于⊙O,
∴∠DAE+∠DFE=180°,
∴∠AEF=∠DAE,
∴四边形DAEF为等腰梯形,
∴AD=EF,
∵AC⊥BD,
∴∠PAM+∠AMP=90°,
AG⊥BC,
∴∠PAM+∠ACB=90°,
∴∠AMP=∠ACB,
∵∠ADB=∠ACB,
∴∠ADB=∠AMP,
∴AD=AM,
∴PD=PM,
∵DF∥AE,
∴∠AMP=∠NDP
∴△NDP≌△AMP,
∴ND=AM,
∴四边形AMND是平行四边形,
∴MN=AD,
∴MN=EF.
点评:本题主要考查了圆的综合题,涉及圆周角,平行四边形的判定及全等三角形的判定,解题的关键是理解题意求出四边形AMND是平行四边形.

练习册系列答案
相关题目
下列事件中,是确定事件的是( )
| A、1小时等于60分钟 |
| B、明天是晴天 |
| C、打雷后会下雨 |
| D、下雨后有彩虹 |
下列运算正确的是( )
| A、(x-y)2=x2-y2 |
| B、x6÷x2=x4 |
| C、x2y+xy2=x3y3 |
| D、x2•y2=(xy)4 |
下列判断错误的是( )
A、0•
| ||||||||||||
B、如果
| ||||||||||||
C、设
| ||||||||||||
D、如果|
|
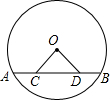 如图,AB是⊙O的弦,点C、D在弦AB上,且AD=BC,联结OC、OD.求证:△OCD是等腰三角形.
如图,AB是⊙O的弦,点C、D在弦AB上,且AD=BC,联结OC、OD.求证:△OCD是等腰三角形. 如图,已知两个不平行的向量
如图,已知两个不平行的向量 如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BD相交于点N,连接MB,ND.
如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BD相交于点N,连接MB,ND.