题目内容

11．已知a，b，c是△ABC的三边，且满足关系式a2+c2=2ab+2bc-2b2，则△ABC是等边三角形．

分析 先把原式化为完全平方的形式再求解．

解答 解：∵原式=a2+c2-2ab-2bc+2b2=0，
a2+b2-2ab+c2-2bc+b2=0，
即（a-b）2+（b-c）2=0，
∴a-b=0且b-c=0，即a=b且b=c，
∴a=b=c．
故△ABC是等边三角形．
故答案为：等边．

点评 此题考查因式分解的实际运用以及非负数的性质，利用完全平方公式因式分解是解决问题的关键．

练习册系列答案
相关题目
1．下列各组数中，互为相反数的是（　　）
A．（-2）-3与23B．（-2）-2与2-2C．-33与（-$\frac{1}{3}$）3D．（-3）-3与（$\frac{1}{3}$）3
2．（1）解方程：x2-4x-3=0                
（2）解不等式组：$\left\{\begin{array}{l}x-3（x-2）≤4\\ \frac{1+2x}{3}＞x-1\end{array}$并将解集在数轴上表示出来．
19．在一幅矩形地毯ABCD的四周镶有宽度都是1米的花边．设矩形地毯AB边长为x米，镶有花边后，整个地毯EFGH中FG边长为y米．
（1）若原地毯ABCD的周长为18米，求y与x的函数关系式（不要求写出自变量的取值范围）；
（2）在（1）的条件下，当整个地毯EFGH的面积是40平方米，且AB＜BC时，AB的长为多少米？
6．判断下列命题是真命题还有假命题．如果是真命题，请证明，如果是假命题，请举出反例．
（1）两个锐角的和是钝角；
（2）在同一平面内，垂直于同一条直线的两条直线互相平行．
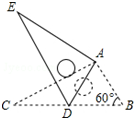16．如图，将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上．若BC=2$\sqrt{3}$，∠B=60°，则CD的长为$\sqrt{3}$．
3．阅读下面材料，并解答下列各题：
在形如ab=N的式子中，我们已经研究过两种情况：
①已知a和b，求N，这是乘方运算；
②已知b和N，求a，这是开方运算；
现在我们研究第三种情况：已知a和N，求b，我们把这种运算叫做对数运算．
定义：如果ab=N（a＞0，a≠1，N＞0），则b叫做以a为底N的对数，记着b=logaN．
例如：因为23=8，所以log28=3；因为2-3=$\frac{1}{8}$，所以log2$\frac{1}{8}$=-3．
（1）根据定义计算：
①log381=4；②log33=1；③log31=0；
④如果logx16=4，那么x=2．
（2）设ax=M，ay=N，则logaM=x，logaN=y（a＞0，a≠1，M、N均为正数），
∵ax•ay=ax+y，∴ax+y=M•N∴logaMN=x+y，
即logaMN=logaM+logaN
这是对数运算的重要性质之一，进一步，我们还可以得出：
logaM1M2M3…Mn=logaM1+logaM2+logaM3+…+logaMn（其中M1、M2、M3、…、Mn均为正数，a＞0，a≠1）
loga$\frac{M}{N}$=logaM-logaN（a＞0，a≠1，M、N均为正数）．仿照上面说明方法，任选一空试说明理由．
20．$（-3{）^{2016}}•（\frac{1}{3}{）^{2015}}$=3．
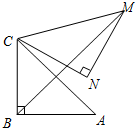1．如图，Rt△ABC中，∠ABC=90°，AB=BC=2，将△ABC绕点C逆时针旋转60°，得到△MNC，连接BM，那么BM的长是$\sqrt{6}+\sqrt{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网