题目内容
19. 在一幅矩形地毯ABCD的四周镶有宽度都是1米的花边.设矩形地毯AB边长为x米,镶有花边后,整个地毯EFGH中FG边长为y米.
在一幅矩形地毯ABCD的四周镶有宽度都是1米的花边.设矩形地毯AB边长为x米,镶有花边后,整个地毯EFGH中FG边长为y米.(1)若原地毯ABCD的周长为18米,求y与x的函数关系式(不要求写出自变量的取值范围);
(2)在(1)的条件下,当整个地毯EFGH的面积是40平方米,且AB<BC时,AB的长为多少米?
分析 (1)利用矩形的周长与边长之间的关系列出函数关系式即可;
(2)根据矩形EFGH的面积计算方法可以列出有关x的一元二次方程求解即可.
解答 解:(1)∵y=BC+2=$\frac{18-2x}{2}$+2
∴y=-x+11
(2)∵矩形EFGH的面积=EF×GH=(x+2)(-x+11)=40
∴-x2+9x+22=40
解得:x=3或x=6
当x=3时,即AB=3,则BC=6;
当x=6时,即AB=6,则BC=3
∵AB<BC
∴x=6(舍去)
答:AB的长为3米.
点评 本题主要考查了一元二次方程的应用,在解题时要能根据矩形的面积有关的信息列出方程是本题的关键.

练习册系列答案
相关题目
14.若菱形两条对角线的长分别为12cm和16cm,则这个菱形的周长为( )
| A. | 10cm | B. | 20cm | C. | 28cm | D. | 40cm |
8.为了提倡低碳经济,某公司为了更好得节约能源,决定购买节省能源的10台新机器.现有甲、乙两种型号的设备供选择,其中每台的价格、工作量如下表:
(1)经预算:该公司购买的节能设备的资金不超过110万元,请列式解答有几种购买方案可供选择;
(2)在(1)的条件下,若每月要求产量不低于2040吨,为了节约资金,请你设计一种最省钱的购买方案.
| 甲型 | 乙型 | |
| 价格(万元/台) | 12 | 10 |
| 产量(吨/月) | 240 | 180 |
(2)在(1)的条件下,若每月要求产量不低于2040吨,为了节约资金,请你设计一种最省钱的购买方案.
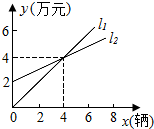 如图,l1表示某品牌电动车厂一天的销售收入与电动车销售量的关系;l2表示该电动车厂一天的销售成本与销售量的关系.
如图,l1表示某品牌电动车厂一天的销售收入与电动车销售量的关系;l2表示该电动车厂一天的销售成本与销售量的关系.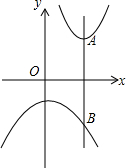 如图,在平面直角坐标系中,抛物线y=a(x-3)2+2(a>0)的顶点为A,过点A作y轴的平行线交抛物线y=-$\frac{1}{3}$x2-2于点B,则A、B两点间的距离为7.
如图,在平面直角坐标系中,抛物线y=a(x-3)2+2(a>0)的顶点为A,过点A作y轴的平行线交抛物线y=-$\frac{1}{3}$x2-2于点B,则A、B两点间的距离为7.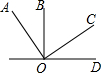 如图,OB⊥OD,OA⊥OC,且∠BOC=58°,则∠AOD的度数为32°.
如图,OB⊥OD,OA⊥OC,且∠BOC=58°,则∠AOD的度数为32°. 如图,一束平行太阳光照射到正方形上,若∠α=28°,则∠β=62°.
如图,一束平行太阳光照射到正方形上,若∠α=28°,则∠β=62°.