题目内容
9. 如图,在△ABC中,AB=AC,∠B=70°,将△ABC绕点C顺时针旋转α(其中0°<α<70°)后得到△A′B′C,连接AA′,则∠AA′B′=50°-$\frac{1}{2}$α(用含α的式子表示).
如图,在△ABC中,AB=AC,∠B=70°,将△ABC绕点C顺时针旋转α(其中0°<α<70°)后得到△A′B′C,连接AA′,则∠AA′B′=50°-$\frac{1}{2}$α(用含α的式子表示).
分析 先由旋转的性质和简单的计算,得到∠CA′B′=∠A=180°-2×70°=40°,根据旋转角和等腰三角形求出.
解答 解:由旋转得,∠CA′B′=∠A=180°-2×70°=40°,
在△CAA′中,∠ACA′=α,CA=CA′,
∴∠CA′A=$\frac{1}{2}$(180°-α)
∴∠AA′B=∠CA′A-∠CA′B′=90°-$\frac{1}{2}$α-40°=50°-$\frac{1}{2}$α.
故答案为50°-$\frac{1}{2}$α.
点评 此题是旋转的性质题,主要考查了旋转的性质和等腰三角形的性质,解本题的关键是用等腰三角形进行计算.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
11.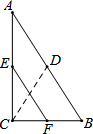 如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点,则DC和EF的大小关系是( )
如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点,则DC和EF的大小关系是( )
 如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点,则DC和EF的大小关系是( )
如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点,则DC和EF的大小关系是( )| A. | DC>EF | B. | DC<EF | C. | DC=EF | D. | 无法比较 |
12.下列一元二次方程有两个相等的实数根的是( )
| A. | x2+1=0 | B. | x2+4x+4=0 | C. | x2+x+(-$\frac{1}{2}$)=0 | D. | x2-x+$\frac{1}{2}$=0 |
18.下列式子中,错误的是( )
| A. | $\sqrt{2}$×$\sqrt{8}$=4 | B. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | C. | $\sqrt{\frac{4}{3}}$=$\frac{2}{3}$$\sqrt{3}$ | D. | $\frac{4\sqrt{18}}{2\sqrt{6}}$=2$\sqrt{3}$ |
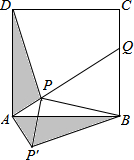 如图,点P是正方形ABCD内一点,PA=1,PB=2$\sqrt{2}$,PD=$\sqrt{10}$,将△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
如图,点P是正方形ABCD内一点,PA=1,PB=2$\sqrt{2}$,PD=$\sqrt{10}$,将△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q. 如图,A,B是4×4网格上的两个格点,在格点中任意放置点C,与点A,点B恰好围成等腰三角形的概率是$\frac{9}{25}$.
如图,A,B是4×4网格上的两个格点,在格点中任意放置点C,与点A,点B恰好围成等腰三角形的概率是$\frac{9}{25}$.