题目内容
11.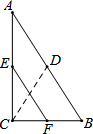 如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点,则DC和EF的大小关系是( )
如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点,则DC和EF的大小关系是( )| A. | DC>EF | B. | DC<EF | C. | DC=EF | D. | 无法比较 |
分析 根据三角形中位线定理证明EF=$\frac{1}{2}$AB,根据直角三角形斜边上的中线等于斜边的一半证明CD=$\frac{1}{2}$AB,得到答案.
解答 解:∵E、F分别为AC、BC的中点,
∴EF=$\frac{1}{2}$AB,
在Rt△ABC中,D是AB的中点,
∴CD=$\frac{1}{2}$AB,
∴CD=EF,
故选:C.
点评 本题考查的是三角形中位线定理和直角三角形的性质,掌握三角形的中位线平行于第三边且等于第三边的一半和直角三角形斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
19.已知一次函数y=kx+1,若y随x的增大而减小,则该函数的图象经过( )
| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第二、三、四象限 | D. | 第一、三、四象限 |
3.对于某个一次函数,当x的值减小1个单位,y的值增加2个单位,则当x的值增加2个单位时,y的值将( )
| A. | 增加4个单位 | B. | 减小4个单位 | C. | 增加2个单位 | D. | 减小2个单位 |
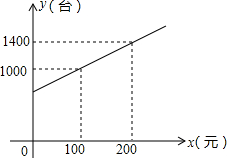 为了拉动内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益p(元)会相应降低且满足:p=-$\frac{1}{5}$x+110(x≥0).
为了拉动内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益p(元)会相应降低且满足:p=-$\frac{1}{5}$x+110(x≥0). (1)计算:|-2|-$\sqrt{9}$+(-$\frac{1}{2}$)-1;
(1)计算:|-2|-$\sqrt{9}$+(-$\frac{1}{2}$)-1; 如图,在△ABC中,AB=AC,∠B=70°,将△ABC绕点C顺时针旋转α(其中0°<α<70°)后得到△A′B′C,连接AA′,则∠AA′B′=50°-$\frac{1}{2}$α(用含α的式子表示).
如图,在△ABC中,AB=AC,∠B=70°,将△ABC绕点C顺时针旋转α(其中0°<α<70°)后得到△A′B′C,连接AA′,则∠AA′B′=50°-$\frac{1}{2}$α(用含α的式子表示).