题目内容
若二次函数的图象y=(m-1)x2+2x与直线y=x-1没有交点,求m的取值范围.
考点:二次函数的性质
专题:计算题
分析:根据二次函数的定义和二次函数图象与一次函数图象的交点问题得到m-1≠0,方程组
无解,再把方程组无解的问题转化为一元二次方程(m-1)x2+x+1=0没有实数根的问题,则根据根的判别式的意义得到12-4(m-1)<0,然后解不等式即可得到满足条件的m的取值范围.
|
解答:解:根据题意m-1≠0,方程组
无解,
所以m≠1且(m-1)x2+2x=x-1没有实数解,
整理得(m-1)x2+x+1=0,
所以△=12-4(m-1)<0,解得m>
,
所以m的取值范围为m>
.
|
所以m≠1且(m-1)x2+2x=x-1没有实数解,
整理得(m-1)x2+x+1=0,
所以△=12-4(m-1)<0,解得m>
| 5 |
| 4 |
所以m的取值范围为m>
| 5 |
| 4 |
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
.也考查了二次函数图象与一次函数图象的交点问题.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

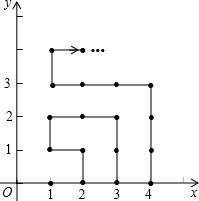 如图,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,其顺序按图中点的坐标分别为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…的规律排列,根据这个规律,第2015个点的横坐标为
如图,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,其顺序按图中点的坐标分别为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…的规律排列,根据这个规律,第2015个点的横坐标为 如图所示,⊙O的半径为R,弦AB,CD相互垂直,连接AD,BC.
如图所示,⊙O的半径为R,弦AB,CD相互垂直,连接AD,BC.
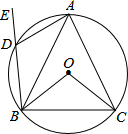 如图所示,⊙O是△ABC的外接圆,D是
如图所示,⊙O是△ABC的外接圆,D是
 实数a在数轴上的位置如图所示,试化简:
实数a在数轴上的位置如图所示,试化简: