题目内容
 如图所示,⊙O的半径为R,弦AB,CD相互垂直,连接AD,BC.
如图所示,⊙O的半径为R,弦AB,CD相互垂直,连接AD,BC.(1)求证:AD2+BC2=4R2;
(2)若AD,BC的长是方程x2-6x+5=0的两个根,求⊙O的半径及点O到AD的距离.
考点:圆周角定理,解一元二次方程-因式分解法,勾股定理
专题:
分析:(1)如图,作⊙O的直径BE,连接AE、CE.利用勾股定理和直角三角形外接圆半径证得结论;
(2)通过解方程求得AD、BC的值;然后将其代入(1)中的等式来求圆的半径;过点O作OF⊥AD于F,由垂径定理和勾股定理进行解答.
(2)通过解方程求得AD、BC的值;然后将其代入(1)中的等式来求圆的半径;过点O作OF⊥AD于F,由垂径定理和勾股定理进行解答.
解答: (1)证明:如图,作⊙O的直径BE,连接AE、CE.
(1)证明:如图,作⊙O的直径BE,连接AE、CE.
∵DE是直径,
∴EC⊥CD.
又∵AB⊥CD,
∴AB∥EC,
∴
=
=CB,
∴AE=CB.
由DE是直径得到:∠EAD=∠ECD=90°.
∵由勾股定理,得AD2=DE2-AE2,
∴AD2+BC2=DE2-AE2+AE2=4R2;
(2)由x2-6x+5=0,得
(x-1)(x-5)=0,
解得 x1=1,x2=5,
∵AD,BC的长是方程x2-6x+5=0的两个根,
∴AD=5,BC=1.
又由(1)知,AD2+BC2=4R2
∴25+1=4R2
则R=
.
如图,过点O作OF⊥AD于F,则FD=
AD=
.
在直角△OFD中,OD=
,FD=
.则由勾股定理知OF=
=
=
.
综上所述,⊙O的半径是
,点O到AD的距离是
.
 (1)证明:如图,作⊙O的直径BE,连接AE、CE.
(1)证明:如图,作⊙O的直径BE,连接AE、CE.∵DE是直径,
∴EC⊥CD.
又∵AB⊥CD,
∴AB∥EC,
∴
 |
| AE |
 |
| BC |
∴AE=CB.
由DE是直径得到:∠EAD=∠ECD=90°.
∵由勾股定理,得AD2=DE2-AE2,
∴AD2+BC2=DE2-AE2+AE2=4R2;
(2)由x2-6x+5=0,得
(x-1)(x-5)=0,
解得 x1=1,x2=5,
∵AD,BC的长是方程x2-6x+5=0的两个根,
∴AD=5,BC=1.
又由(1)知,AD2+BC2=4R2
∴25+1=4R2
则R=
| ||
| 2 |
如图,过点O作OF⊥AD于F,则FD=
| 1 |
| 2 |
| 5 |
| 2 |
在直角△OFD中,OD=
| ||
| 2 |
| 5 |
| 2 |
| DO2-FD2 |
|
| 1 |
| 2 |
综上所述,⊙O的半径是
| ||
| 2 |
| 1 |
| 2 |
点评:本题考查了圆周角定理,因式分解法解一元二次方程以及勾股定理.根据题意作出辅助线是解题的难点.

练习册系列答案
相关题目
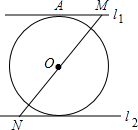 如图所示,直线l1∥l2,点M、N分别为l1、l2上的点,点O为MN的中点,以点O为圆心作⊙O与l1相切,切点为A.求证:⊙O与L2相切.
如图所示,直线l1∥l2,点M、N分别为l1、l2上的点,点O为MN的中点,以点O为圆心作⊙O与l1相切,切点为A.求证:⊙O与L2相切.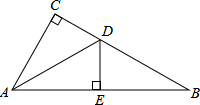 如图,在△ABC中,∠C=90°,AC=
如图,在△ABC中,∠C=90°,AC=