题目内容
抛物线y=x2-x-6在x轴上截得的线段长度是 ．
考点：抛物线与x轴的交点
专题：
分析：先把抛物线方程转化为两点式，则易求抛物线与x轴交点的横坐标，则由两个交点坐标来求物线y=x2-x-6在x轴上截得的线段长度．
解答：解：∵y=x2-x-6=（x-3）（x+2），
∴抛物线与x轴两交点的横坐标分别是3、-2，
∴抛物线y=x2-x-6在x轴上截得的线段长度是：|3|+|-2|=5．
故答案是：5．
∴抛物线与x轴两交点的横坐标分别是3、-2，
∴抛物线y=x2-x-6在x轴上截得的线段长度是：|3|+|-2|=5．
故答案是：5．
点评：本题考查的是抛物线与x轴的交点问题，此题也可以由根与系数的关系得到x1+x2及x1•x2的值，再由完全平方公式求解即可．
练习册系列答案
相关题目
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，令x0=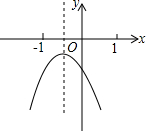
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，在下列五个结论中：
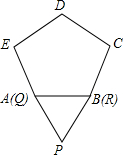如图，将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动（点Q、点R分别与点A、点B重合），当△PQR第一次回到原来的起始位置时（顶点位置与原来相同），点P所经过的路线长为
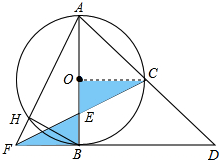如图，以AB为直径的⊙O切△AFD的边FD于点B，AD交⊙O于点C，且C是弧AB的中点，CF交AB于点E，且E为OB中点．若AF交⊙O于点H，连接BH，若OA=4，求BH的长．
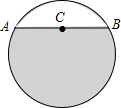某居民区一处圆形下水管道破裂需要更换，下水管道横截面如图所示，已知污水面宽AB=60m，C为AB中点，且C点距管道底部的距离为90cm，求圆形管道的直径．