题目内容
如图甲,在正方形ABCD和正方形BEFG中,点A,B,E在同一条直线上,连接DF,且P是线段DF的中点,连接PG,PC.
(1)如图甲中,PG与PC的位置关系是 ,数量关系是 ;
(2)如图乙将条件“正方形ABCD和正方形BEFG”改为“矩形ABCD和矩形BEFG”其它条件不变,求证:PG=PC.
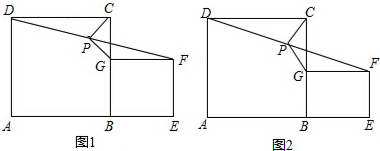
(1)如图甲中,PG与PC的位置关系是
(2)如图乙将条件“正方形ABCD和正方形BEFG”改为“矩形ABCD和矩形BEFG”其它条件不变,求证:PG=PC.

考点:全等三角形的判定与性质,矩形的性质,正方形的性质
专题:
分析:(1)延长GP交CD于H,可证△DPH≌△GPF,即可求得DH=FG,CH=CG,根据等腰三角形底边三线合一可得PC=PG,PC⊥PG;
(2)延长GP交CD于H,可证△DPH≌△GPF,即可求得PH=PG,根据直角三角形底边斜边中线等于斜边一半性质即可解题.
(2)延长GP交CD于H,可证△DPH≌△GPF,即可求得PH=PG,根据直角三角形底边斜边中线等于斜边一半性质即可解题.
解答:证明:(1)PG⊥PC,PG=PC;
延长GP交CD于H,
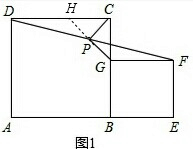
∵P是DF中点,∴DP=FP,
∵点ABE在同一直线上,
∴DC∥GF,
∴∠FDC=∠GFP,
∵在△DPH和△GPF中,
,
∴△DPH≌△GPF(ASA)
∴HP=GP,GF=DH,
∴CH=CG,
又∵∠HCG=90°,
∴RT△HCG中,P为HG中点,
∴PC=
GH=PG,PC⊥PG;
(2)延长GP交CD于H,
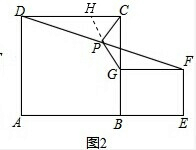
∵P是DF中点,∴DP=FP,
∵点ABE在同一直线上,
∴DC∥GF,
∴∠FDC=∠GFP
∵在△DPH和△GPF中,
,
∠HPD=∠GPF,
∴△DPH≌△GPF(ASA)
∴HP=GP,
又∵∠HCG=90°,
∴RT△HCG中,P为HG中点,
∴PC=
GH=PG,
即:PG=PC.
延长GP交CD于H,

∵P是DF中点,∴DP=FP,
∵点ABE在同一直线上,
∴DC∥GF,
∴∠FDC=∠GFP,
∵在△DPH和△GPF中,
|
∴△DPH≌△GPF(ASA)
∴HP=GP,GF=DH,
∴CH=CG,
又∵∠HCG=90°,
∴RT△HCG中,P为HG中点,
∴PC=
| 1 |
| 2 |
(2)延长GP交CD于H,

∵P是DF中点,∴DP=FP,
∵点ABE在同一直线上,
∴DC∥GF,
∴∠FDC=∠GFP
∵在△DPH和△GPF中,
|
∠HPD=∠GPF,
∴△DPH≌△GPF(ASA)
∴HP=GP,
又∵∠HCG=90°,
∴RT△HCG中,P为HG中点,
∴PC=
| 1 |
| 2 |
即:PG=PC.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△DPH≌△GPF是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
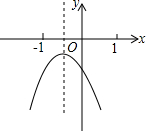 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中: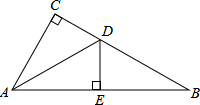 如图,在△ABC中,∠C=90°,AC=
如图,在△ABC中,∠C=90°,AC=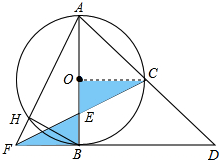 如图,以AB为直径的⊙O切△AFD的边FD于点B,AD交⊙O于点C,且C是弧AB的中点,CF交AB于点E,且E为OB中点.若AF交⊙O于点H,连接BH,若OA=4,求BH的长.
如图,以AB为直径的⊙O切△AFD的边FD于点B,AD交⊙O于点C,且C是弧AB的中点,CF交AB于点E,且E为OB中点.若AF交⊙O于点H,连接BH,若OA=4,求BH的长. 如图,A,B,C,D是⊙O上的四点,且∠BCD=100°,求∠BOD(弧BCD所对的圆心角)和∠BAD的大小.
如图,A,B,C,D是⊙O上的四点,且∠BCD=100°,求∠BOD(弧BCD所对的圆心角)和∠BAD的大小.