题目内容
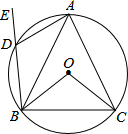 如图所示,⊙O是△ABC的外接圆,D是
如图所示,⊙O是△ABC的外接圆,D是 |
| AB |
考点:圆内接四边形的性质,圆周角定理
专题:
分析:先根据圆内接四边形的性质求出∠ACB的度数,再由AB=AC可得出∠ABC的度数,根据三角形内角和定理求出∠BAC的度数,再由圆周角定理即可得出结论.
解答:解:∵四边形ABDC内接圆⊙O,∠ADE=65°,
∵∠ACB=65°.
∵AB=AC,
∴∠ABC=∠ACB=65°,
∴∠BAC=180°-65°-65°=50°.
∵∠BAC与∠BOC是同弧所对的圆周角与圆心角,
∴∠BOC=2∠BAC=100°.
∵∠ACB=65°.
∵AB=AC,
∴∠ABC=∠ACB=65°,
∴∠BAC=180°-65°-65°=50°.
∵∠BAC与∠BOC是同弧所对的圆周角与圆心角,
∴∠BOC=2∠BAC=100°.
点评:本题考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
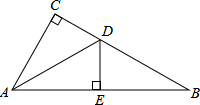 如图,在△ABC中,∠C=90°,AC=
如图,在△ABC中,∠C=90°,AC=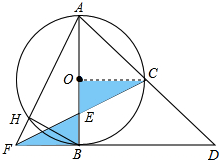 如图,以AB为直径的⊙O切△AFD的边FD于点B,AD交⊙O于点C,且C是弧AB的中点,CF交AB于点E,且E为OB中点.若AF交⊙O于点H,连接BH,若OA=4,求BH的长.
如图,以AB为直径的⊙O切△AFD的边FD于点B,AD交⊙O于点C,且C是弧AB的中点,CF交AB于点E,且E为OB中点.若AF交⊙O于点H,连接BH,若OA=4,求BH的长.