题目内容
1.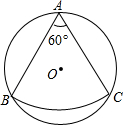 如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )
如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )| A. | $\frac{\sqrt{3}}{6}$m | B. | $\frac{\sqrt{3}}{12}$m | C. | $\frac{\sqrt{3}}{2}$m | D. | 1m |
分析 连接OA,作OD⊥AB于点D,利用三角函数即可求得AD的长,则AB的长可以求得,然后利用弧长公式即可求得弧长,即底面圆的周长,再利用圆的周长公式即可求得半径.
解答 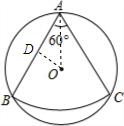 解:连接OA,作OD⊥AB于点D.
解:连接OA,作OD⊥AB于点D.
在直角△OAD中,OA=1,∠OAD=$\frac{1}{2}$∠BAC=30°,
则AD=OA•cos30°=$\frac{\sqrt{3}}{2}$.
则AB=2AD=$\sqrt{3}$,
则扇形的弧长是:$\frac{60π\sqrt{3}}{180}$=$\frac{\sqrt{3}}{3}π$,
设底面圆的半径是r,则2π×1=$\frac{\sqrt{3}}{3}π$,
解得:r=$\frac{\sqrt{3}}{6}$.
故答案是:A.
点评 本题考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.

练习册系列答案
相关题目
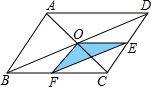 如图,已知平行四边形ABCD的面积是32,点0是平行四边形ABCD对角线的交点,OE∥AD交CD于点E,OF∥AB于点F,那么△EOF的面积是4.
如图,已知平行四边形ABCD的面积是32,点0是平行四边形ABCD对角线的交点,OE∥AD交CD于点E,OF∥AB于点F,那么△EOF的面积是4. 如图,一张纸片的形状为直角三角形,其中∠C=90°,AC=12cm,BC=16cm,沿直线AD折叠该纸片,使直角边AC与斜边上的AE重合,则CD的长为6cm.
如图,一张纸片的形状为直角三角形,其中∠C=90°,AC=12cm,BC=16cm,沿直线AD折叠该纸片,使直角边AC与斜边上的AE重合,则CD的长为6cm. 如图,把边长为2的正方形剪成四个完全一样的直角三角形,在下面对应的正方形网格(每个小正方形的边长均为1)中画出用这四个直角三角形按要求分别拼成的新的多边形.(要求全部用上,互不重叠,互不留隙).
如图,把边长为2的正方形剪成四个完全一样的直角三角形,在下面对应的正方形网格(每个小正方形的边长均为1)中画出用这四个直角三角形按要求分别拼成的新的多边形.(要求全部用上,互不重叠,互不留隙).
 如图,四边形ABCD是平行四边形,连接对角线AC,E、F是对角线AC上两点,满足AE=CF,求证:四边形DEBF是平行四边形.
如图,四边形ABCD是平行四边形,连接对角线AC,E、F是对角线AC上两点,满足AE=CF,求证:四边形DEBF是平行四边形.