题目内容
11.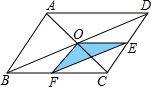 如图,已知平行四边形ABCD的面积是32,点0是平行四边形ABCD对角线的交点,OE∥AD交CD于点E,OF∥AB于点F,那么△EOF的面积是4.
如图,已知平行四边形ABCD的面积是32,点0是平行四边形ABCD对角线的交点,OE∥AD交CD于点E,OF∥AB于点F,那么△EOF的面积是4.
分析 设平行四边形ABCD的面积是a,可求得△BCD的面积,又由OE∥AD交CD于点E,OF∥AB于点F,易得△DOE∽△DBC,△BOF∽△BDC,△CEF∽△CDB,进而得出△EOF的面积.
解答 解:∵平行四边形ABCD的面积是32,
∴S△BCD=$\frac{1}{2}$S?ABCD=16,OB=OD,
∵OE∥AD,OF∥AB,
∴△DOE∽△DBC,△BOF∽△BDC,
∴S△DOE=$\frac{1}{4}$S△BCD=4,S△BOF=$\frac{1}{4}$S△BCD=4,
∴DE=CE,BF=CF,
∴EF∥BD,EF=$\frac{1}{2}$BD,
∴△CEF∽△CDB,
∴S△CEF=$\frac{1}{4}$S△BCD=4,
∴S△EOF=16-4-4-4=4,
故答案为:4.
点评 此题考查了平行四边形的性质以及相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
6.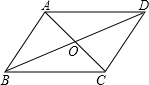 如图,AC,BD是平行四边形ABCD的对角线,AC与BD交于点O,若AC=4,BD=5,BC=3,则△BOC的周长是( )
如图,AC,BD是平行四边形ABCD的对角线,AC与BD交于点O,若AC=4,BD=5,BC=3,则△BOC的周长是( )
 如图,AC,BD是平行四边形ABCD的对角线,AC与BD交于点O,若AC=4,BD=5,BC=3,则△BOC的周长是( )
如图,AC,BD是平行四边形ABCD的对角线,AC与BD交于点O,若AC=4,BD=5,BC=3,则△BOC的周长是( )| A. | 7.5 | B. | 6 | C. | 12 | D. | 10 |
1.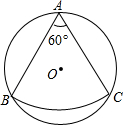 如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )
如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )
 如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )
如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )| A. | $\frac{\sqrt{3}}{6}$m | B. | $\frac{\sqrt{3}}{12}$m | C. | $\frac{\sqrt{3}}{2}$m | D. | 1m |
 如图,∠1=∠2,∠3=∠4,∠ABC与∠ADC是否相等,为什么?
如图,∠1=∠2,∠3=∠4,∠ABC与∠ADC是否相等,为什么?
 线段PQ在直线l上运动,试确定PQ的位置,使点A出发经过PQ到达点B的路线最短.
线段PQ在直线l上运动,试确定PQ的位置,使点A出发经过PQ到达点B的路线最短.